Let the tangent to the circle C1 : x2 + y2 = 2 at the point M(1, 1) intersect the circle <math><mrow><msub><mrow><mi>C</mi></mrow><mrow><mn>2</mn></mrow></msub><mo>:</mo><msup><mrow><mrow><mo>(</mo><mrow><mi>x</mi><mo>−</mo><mn>3</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></math> + <math><mrow><msup><mrow><mrow><mo>(</mo><mrow><mi>y</mi><mo>−</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mo>=</mo><mn>5</mn><mo>,</mo></mrow></math> at two distinct points A and B. If the tangents to C2 at the points A and B intersect at N, then the area of the triangle ANB is equal to:

Tangent to C1 at (-1, 1) is T = 0 x(-1) + 4(1) = 2-x + y = 2find OP by dropping  from (3, 2) to centreOP = |3−2+22|=32AP = r2−OP2=5−92=12tanθ=OPAP=3/21/2=3area of ΔABN=12AN2⋅sin2θAN = 53=12⋅59⋅(2tanθ1+tan2θ)=52.9×2.31+32=16sin = APAN

Let the tangent to the circle C1 : x2 + y2 = 2 at the point M(1, 1) intersect the circle&nbsp;<math><mrow><msub><mrow><mi>C</mi></mrow><mrow><mn>2</mn></mrow></msub><mo>:</mo><msup><mrow><mrow><mo>(</mo><mrow><mi>x</mi><mo>−</mo><mn>3</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>&nbsp;+&nbsp;<math><mrow><msup><mrow><mrow><mo>(</mo><mrow><mi>y</mi><mo>−</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mo>=</mo><mn>5</mn><mo>,</mo></mrow></math>&nbsp;at two distinct points A and B. If the tangents to C2 at the points A and B intersect at N, then the area of the triangle ANB is equal to:

Ask & Answer Question

Maths Class 12th Conic Sections Maths NCERT Exemplar Solutions Class 12th Chapter Eleven

Let the tangent to the circle C₁ : x² + y² = 2 at the point M(1, 1) intersect the circle $C_{2} : {(x - 3)}^{2}$ + ${(y - 2)}^{2} = 5,$ at two distinct points A and B. If the tangents to C₂at the points A and B intersect at N, then the area of the triangle ANB is equal to:

Option 1 -

$\frac{1}{2}$

Option 2 -

$\frac{2}{3}$

Option 3 -

$\frac{1}{6}$

Option 4 -

$\frac{5}{3}$

2 Views | Posted 2 months ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

2 months ago

Correct Option - 3

Detailed Solution: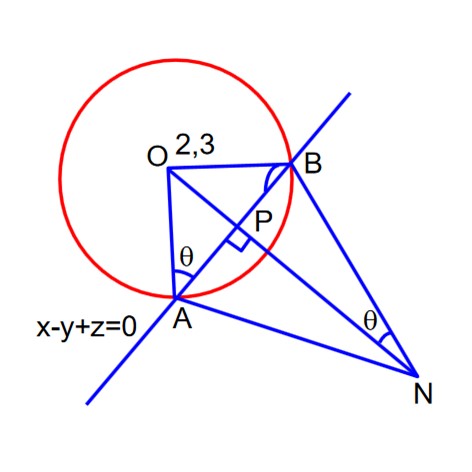

Tangent to C₁ at (-1, 1) is T = 0

x(-1) + 4(1) = 2

-x + y = 2

find OP by dropping from (3, 2) to centre

OP = $| \frac{3 - 2 + 2}{\sqrt[]{2}} | = \frac{3}{\sqrt[]{2}}$

AP = $\sqrt[]{r^{2} - O P^{2}}$

$= \sqrt[]{5 - \frac{9}{2}} = \frac{1}{\sqrt[]{2}}$

$t a n θ = \frac{O P}{A P} = \frac{3 / \sqrt[]{2}}{1 / \sqrt[]{2}} = 3$

area of $Δ A B N = \frac{1}{2} A N^{2} \cdot s i n 2 θ$

AN = $\frac{\sqrt[]{5}}{3}$

$= \frac{1}{2} \cdot \frac{5}{9} \cdot (\frac{2 t a n θ}{1 + t a n^{2} θ})$

$= \frac{5}{2.9} \times \frac{2.3}{1 + 3^{2}} = \frac{1}{6}$

sin = $\frac{A P}{A N}$

0 Upvotes 0 Downvotes

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Let the tangent to the circle C₁ : x² + y² = 2 at the point M(1, 1) intersect the circle $C_{2} : {(x - 3)}^{2}$ + ${(y - 2)}^{2} = 5,$ at two distinct points A and B. If the tangents to C₂at the points A and B intersect at N, then the area of the triangle ANB is equal to:

1 Answer

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

Let the tangent to the circle C1 : x2 + y2 = 2 at the point M(1, 1) intersect the circle C2:(x−3)2 + (y−2)2=5, at two distinct points A and B. If the tangents to C2 at the points A and B intersect at N, then the area of the triangle ANB is equal to:

1 Answer

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

Let the tangent to the circle C₁ : x² + y² = 2 at the point M(1, 1) intersect the circle $C_{2} : {(x - 3)}^{2}$ + ${(y - 2)}^{2} = 5,$ at two distinct points A and B. If the tangents to C₂at the points A and B intersect at N, then the area of the triangle ANB is equal to: