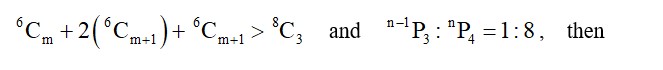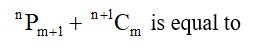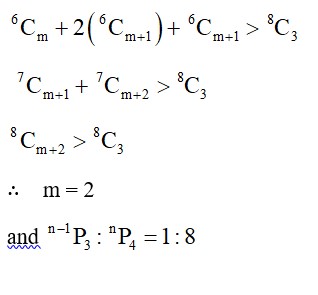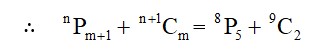Permutation and Combination Exercise 6.1 Solutions
1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed?
Permutation and Combination Exercise 6.1 Solutions
1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed?
1. i. Since repetition of number is allowed and there are five numbers which can be used to form the necessary 3-digit numbers we can have five numbers that can fill the ones, tens and hundreds place.
So, total number of possible 3-digit number = 5 * 5 * 5 = 125
ii. Since repetition of number is not a
Similar Questions for you
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
x + 2y + 3z = 42
0 x + 2y = 42 ->22 cases
1 x + 2y = 39 ->19 cases
2 x + 2y = 36 ->19 cases
3 x + 2y = 33 ->17 cases
4 x + 2y = 30 ->16 cases
5 x + 2y = 27 ->14 cases
6 x + 2y = 24
Total ways to partition 5 into 4 parts are:
5 0
4 1 0
3 2 0
3 1 0
2 1
51 Total way
After giving 2 apples to each child 15 apples left now 15 apples can be distributed in
15+3–1C2 = 17C2 ways
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Maths Ncert Solutions class 11th 2026
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering