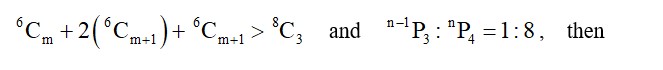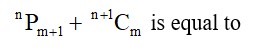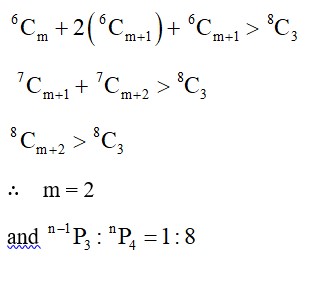The number of 7-digit numbers which are multiples of 1 and are formed using all the digits 1, 2, 3, 4, 5, 7 and 9 is

Start with

(1) $\overline{E}:\frac{6!}{2!}=360$  

(2)    $\overline{GE}:\frac{5!}{2!},$ $\overline{GN}:\frac{5!}{2!}$  

(3) GTE : 4!, GTN: 4!, GTT : 4!

(4) GTWENTY = 1

⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553

x + 2y + 3z = 42

0    x + 2y = 42 ->22 cases

1    x + 2y = 39 ->19 cases

2    x + 2y = 36 ->19 cases

3    x + 2y = 33 ->17 cases

4    x + 2y = 30 ->16 cases

5    x + 2y = 27 ->14 cases

6    x + 2y = 24 ->13 cases

7    x + 2y = 21 ->11 cases

8    x + 2y = 18 ->10 cases

9    x + 2y = 15 ->8 cases

10  x + 2y =12 -> 7 cases

11  x + 2y = 9 -> 5 cases

12  x + 2y = 6 -> 4 cases

13  x + 2y = 3 -> 2 cases

14  x + 2y = 0 -> 1 cases.

Total ways to partition 5 into 4 parts are:

5 0 

4 1 0  $\frac{5!}{4!}=5$

3 2 0 $\frac{5!}{3!\cdot 2!}=10$

3 1 0 $\frac{5!}{2!2!2!}=15$

2 1 $\frac{5!}{2!\times 3!}=10$

51 Total way

After giving 2 apples to each child 15 apples left now 15 apples can be distributed in
^15+3–1C₂ = ¹⁷C₂ ways

  $=\frac{17*16}{2}=136$          

$=8*7*6*5*4+\frac{9*8}{2}$

= 6756