Search Colleges, Courses, Exams, Questions and Articles

Ask a query on 8879100846 Ask Login | Sign Up

 

 

› Ask & Answer › Question

The sum of the surface areas of a rectangular parallelepiped with sides x, 2x, and and a sphere is given to be constant. Prove that the sum of their volumes is minimum if x is equal to three times the radius of the sphere. Also, find the minimum value of the sum of their volumes.

0 3 Views | Posted 3 months ago
Asked by Shiksha User

  • 1 Answer

  • A

    Answered by

    alok kumar singh | Contributor-Level 10

    3 months ago

    This is a Long Answer Type Question as classified in NCERT Exemplar

    Sol:

       

    L e t     ' r '     b e     t h e     r a d i u s     o f     t h e     s p h e r e . ∴     S u r f a c e     a r e a     o f     t h e     s p h e r e = 4 π r 2 V o l u m e     o f     t h e     s p h e r e = 4 3 π r 3 T h e     s i d e s     o f     t h e     p a r a l l e l o p i p e d     a r e     x ,   2 x     a n d     x 3 ∴         I t s     s u r f a c e     a r e a = 2 [ x × 2 x + 2 x × x 3 + x × x 3 ]                                                                                       = 2 [ 2 x 2 + 2 x 2 3 + x 2 3 ] = 2 [ 2 x 2 + x 2 ]                                                                                         = 2 [ 3 x 2 ] = 6 x 2 V o l u m e     o f     t h e     p a r a l l e l o p i p e d = x × 2 x × x 3 = 2 3 x 3 A s     p e r     t h e     c o n d i t i o n s     o f     t h e     q u e s t i o n , surface  area  of  the  parallelopiped+surface  area  of  the  sphere=constant ⇒                       6 x 2 + 4 π r 2 = K ( constant )           ⇒ 4 π r 2 = K − 6 x 2 ∴                                                                 r 2 = K − 6 x 2 4 π                                                                                                                                           … ( i ) N o w     l e t                                     V = V o l u m e     o f     t h e     p a r a l l e l o p i p e d + V o l u m e     o f     t h e     s p h e r e ⇒                                                               V = 2 3 x 3 + 4 3 π r 3 ⇒                                                               V = 2 3 x 3 + 4 3 π [ K − 6 x 2 4 π ] 3 / 2                   [ F r o m     e q . ( i ) ] ⇒ &thi

    S q u a r i n g     b o t h     s i d e s ,     w e     g e t ⇒               4 π x 2 = 9 ( K − 6 x 2 )                 ⇒ 4 π x 2 = 9 K − 5 4 x 2 ⇒                   4 π x 2 + 5 4 x 2 = 9 K ⇒                 K = 4 π x 2 + 5 4 x 2 9                                                                       ( i i ) ⇒                 2 x 2 ( 2 π + 2 7 ) = 9 K ∴                                                           x 2 = 9 K 2 ( 2 π + 2 7 ) = 3 N o w     f r o m     e q . ( i )     w e     h a v e                                                               r 2 = K − 6 x 2 4 π ⇒                                                     r 2 = 4 π x 2 + 5 4 x 2 9 − 6 x 2 4 π ⇒                                                     r 2 = 4 π x 2 + 5 4 x 2 − 5 4 x 2 9 × 4 π = 4 π x 2 9 × 4 π = x 2 9         ⇒ r = x 3         ∴ x = 3 r N o w     w e     h a v e               d V d x = 2 x 2 − 3 x ( K − 6 x 2 ) 1 / 2

                                              = 1 2 − 3 4 K π + 5 4 K − 1 0 8 K 4 π + 5 4                                           = 1 2 − 3 [ 4 K π − 5 4 K 4 π + 5 4 ]                                           = 1 2 − 3 [ 4 K π − 5 4 K . ]                                           = 1 2 − 6 [ 2 π − 2 7 . ]                                           = 1 2 + 6 K [ 2 7 − 2 π . ] > 0                           [ ? 2 7 − 2 π > 0 ] ∴  d2Vdx2>0  So,  it  is  minima. Hence,  the  sum  of  volume  is  min

Similar Questions for you

If the normal to the curve y(x) = ∫(from 2 to x) (2t² - 15t + 10)dt at a point (a, b) is parallel to the line x + 3y = -5, a > 1, then the value of |a + 6b| is equal to..........
R
Raj Pandey

y (x) = ∫? (2t² - 15t + 10)dt
dy/dx = 2x² - 15x + 10.
For tangent at (a, b), slope is m = dx/dy = 1 / (dy/dx) = 1 / (2a² - 15a + 10).
Given slope is -1/3.
2a² - 15a + 10 = -3
2a² - 15a + 13 = 0 (The provided solution has 2a²-15a+7=0, suggesting a different problem or a typo)
Following the image: 2a² - 15a + 7 = 0
(2a - 1) (a - 7) = 0
a = 1/2 or a = 7.
a = 1/2 Rejected as a > 1. So a = 7.
b = ∫? (2t² - 15t + 10)dt = [2t³/3 - 15t²/2 + 10t] from 0 to 7.
6b = [4t³ - 45t² + 60t] from 0 to 7 = 4 (7)³ - 45 (7)² + 60 (7) = 1372 - 2205 + 420 = -413.
|a + 6b| = |7 - 413| = |-406|

...more

If the tangent to the curve, y = f(x) = xlog? x, (x > 0) at a point (c, f(c)) is parallel to the line - segment joining the points (1,0) and (e, e) then c is equal to:
R
Raj Pandey

f' (c) = 1 + lnc = e/ (e-1)
lnc = e/ (e-1) - 1 = (e - (e-1)/ (e-1) = 1/ (e-1)
c = e^ (1/ (e-1)

The lengths of the sides of a triangle are 10 + x2, 10 + x2 and 20 – 2x2. If for x = k, the area of the triangle is maximum, then 3k2 is equal to:
R
Raj Pandey

C D = ( 1 0 + x 2 ) 2 − ( 1 0 − x 2 ) 2 = 2 1 0 | x |

Area 

= 1 2 × C D × A B = 1 2 × 2 1 0 | x | ( 2 0 − 2 x 2 )

⇒ 1 0 − x 2 = 2 x

3x2 = 10

 x = k

3k2 = 10

Let F1(A,B,C) = ( A ∧ ∼ B ) ∨ [ ∼ C ∧ ( A ∨ B ) ] ∨ ∼ A     a n d     F 2 ( A , B ) = ( A ∨ B ) ∨ ( B → ∼ A )  be two logical expressions. Then:
V
Vishal Baghel

By truth table

So F1 (A, B, C) is not a tautology

Now again by truth table

So      F2 (A, B) be a tautology.

The triangle of maximum area that can be inscribed in a given circle of radius ‘r’ is:
V
Vishal Baghel

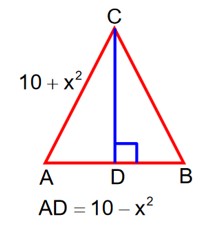
From option let it be isosceles where AB = AC then

x = r 2 − ( h − r ) 2            

=  r 2 − h 2 − r 2 + 2 r h

x = 2 h r − h 2 . . . . . . . . ( i )

 Now ar ( Δ A B C ) = Δ = 1 2 B C × A L

Δ = 1 2 × 2 2 h r − a 2 × h        

then  x = 2 × 3 r 2 × r − 9 r 2 4 = 3 2 r         f r o m ( i )

⇒ B C = 3 r    

So A B = h 2 + x 2 = 9 r 2 4 + 3 r 2 4 = 3 r .

Hence Δ be equilateral having each side of length 3 r .

Get authentic answers from experts, students and alumni that you won't find anywhere else

Sign Up on Shiksha

On Shiksha, get access to

  • 65k Colleges
  • 1.2k Exams
  • 688k Reviews
  • 1800k Answers

Learn more about...

Share Your College Life Experience

Write a Review

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Ask Now
Community GuidelinesUser Points System
QuestionsDiscussionsTags
×

This website uses Cookies and related technologies for the site to function correctly and securely, improve & personalise your browsing experience, analyse traffic, and support our marketing efforts and serve the Core Purpose. By continuing to browse the site, you agree to Privacy Policy and Cookie Policy.

Need guidance on career and education? Ask our experts

Characters 0/140

The Answer must contain atleast 20 characters.

Add more details

Characters 0/300

The Answer must contain atleast 20 characters.

Keep it short & simple. Type complete word. Avoid abusive language. Next

Your Question

Edit

Add relevant tags to get quick responses. Cancel Post