Maths Three Dimensional Geometry Class 12th Ncert Solutions Maths class 12th NCERT Maths 12th NCERT

What are the important topics in Three Dimensional Geometry Class 12 for board exams?

5 Views | Posted 5 months ago

1 Answer

Answered by

5 months ago

3D Geometry holds good weightage in the class 12 board exams, So students must be aware of the important topics that can be asked in the exams. Class 12 Three Dimensional Geometry chapter covers many important topics like direction cosines and ratios, equations of a line, angles between two lines, skew lines, the shortest distance, and equations of planes. Students can use our NCERT Solutions for Class 12 3D Geometry for clear understanding of these topics.

0 Upvotes 0 Downvotes

Similar Questions for you

If $\int_{}^{} (\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

Then the value of 'α' is equal to

alok kumar singh

$\int_{- \frac{π}{2}}^{\frac{π}{2}} (\frac{x^{2} c o s x}{1 + π^{2}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} {(\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) + (\frac{x^{2} c o s x}{1 + π^{- x}} + \frac{1 + s i n^{2} x}{1 + e^{- {(s i n x)}^{2023}}})} d x$

$= \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} (x^{2} c o s x + 1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} x^{2} c o s x d x + \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$ ....(1)

Let $I_{1} = \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x$

$I_{1} = \int_{0}^{\frac{π}{2}} 1 \cdot d x + \int_{0}^{\frac{π}{2}} (\frac{1 - c o s 2 x}{2}) d x$

$I_{1} = \frac{π}{2} + \frac{1}{2} [\frac{π}{2} + 0]$

$I_{1} = \frac{3 π}{4}$

Let $I_{2} = \int_{0}^{\frac{π}{2}} x^{2} c o s x d x$

$I_{2} = {[x^{2} (s i n x) - \int 2 x \int c o s x d x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} (s i n x) - 2 \int x s i n x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (x (- c o s x) + \int c o s x)]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (- x c o s x + s i n x)]}_{0}^{\frac{π}{2}}$

$I_{2} = (\frac{π^{2}}{4} - 2)$

Put l₁ and l₂ in (1)

$\frac{π^{2}}{4} - 2 + \frac{3 π}{4}$

$\frac{π^{2}}{4} + \frac{3 π}{4} - 2$

$\frac{π}{4} (π + 3) - 2$

α = 3

If $| \vec{a} | = 1$ , $| \vec{b} | = 4$ $\vec{a} \cdot \vec{b} = 2$ and $\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$ Then the angle between $\vec{b}$ and $\vec{c}$ is

alok kumar singh

Given $| \vec{a} | = 1$ , $| \vec{b} | = 4$ , $\vec{a} \cdot \vec{b} = 2$

$\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$

Dot product with $\vec{a}$ on both sides

$\vec{c} \cdot \vec{a} = - 6$ ... (1)

Dot product with $\vec{b}$ on both sides

$\vec{b} \cdot \vec{c} = - 48$ ... (2)

$\vec{c} \cdot \vec{c} = 4 {| \vec{a} \times \vec{b} |}^{2} + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [{| \vec{a} |}^{2} \cdot {| \vec{b} |}^{2} - {(\vec{a} \cdot \vec{b})}^{2}] + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [(1) {(4)}^{2} - (4)] + 9 (16)$

${| \vec{c} |}^{2} = 4 [12] + 144$

${| \vec{c} |}^{2} = 48 + 144$

${| \vec{c} |}^{2} = 192$

$c o s θ = \frac{\vec{b} \cdot \vec{c}}{| \vec{b} | | \vec{c} |}$

$c o s θ = \frac{- 48}{\sqrt[]{192} \cdot 4}$

$c o s θ = \frac{- 48}{8 \sqrt[]{3} \cdot 4}$

$c o s θ = \frac{- 3}{2 \sqrt[]{3}}$

$c o s θ = \frac{- \sqrt[]{3}}{2}$ $θ = c o s^{- 1} (\frac{- \sqrt[]{3}}{2})$

If the foot of perpendicular from (1, 2, 3) to the line $\frac{x + 1}{2} = \frac{y - 2}{5} = \frac{z - 4}{1}$ is (a, b, g) then find a + b + g

alok kumar singh

(a – 1) × 2 + (b – 2) × 5 + (g – 3) × 1 = 0

2a + 5b + g – 15 = 0

Also, P lie on line

a + 1 = 2λ

b – 2 = 5λ

g – 4 = λ

2 (2λ – 1) + 5 (5λ + 2) + λ + 4 – 15 = 0

4λ + 25λ + λ – 2 + 10 + 4 – 15 = 0

30λ – 3 = 0

$λ = \frac{1}{10}$

a + b + g = (2λ – 1) + (5λ + 2) + (λ + 4)

$= 8 λ + 5 = \frac{8}{10} + 5 = 5.8$

If (α, β, γ) is mirror image of the point (2, 3, 4) with respect to the line $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4}$ Then 2α + 3β + 4γ is

alok kumar singh

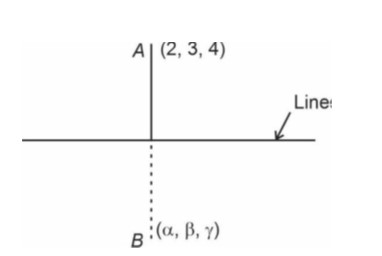
Take $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} = λ$

x = 2λ + 1, y = 3λ + 2, z = 4λ + 3

$\vec{A B}$ = (α − 2) $\hat{i}$ + (β − 3) $\hat{j}$ + (γ − 4) $\hat{k}$

Now,

(α − 2) ⋅ 2 + (β − 3) ⋅3 + (γ − 4) ⋅ 4 = 0

2α − 4 + 3β − 9 + 4γ −16 = 0

⇒ 2α + 3β + 4γ = 29

Let $λ$ be an integer. IF the shortest distance between the lines $x - λ = 2 y - 1 = - 2 z$ and $x = y + 2 λ = z - λ i s \frac{\sqrt[]{7}}{2 \sqrt[]{2}}$ , then the value of $| λ | i s . . . . . . . . . . . . . . . . . . .$

Vishal Baghel

$L_{1} = \frac{x - λ}{1} = \frac{y - \frac{1}{2}}{\frac{1}{2}} = \frac{z}{- \frac{1}{2}}$

$∴ S D = \frac{| - 2 λ + 3 (2 λ + \frac{1}{2}) + λ |}{\sqrt[]{14}} = \frac{| 5 λ + \frac{3}{2} |}{\sqrt[]{14}}$

$5 λ + \frac{3}{2} = - \frac{7}{2} \Rightarrow 5 λ = - 5 \Rightarrow λ = - 1$

$∴ | λ | = 1$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

What are the important topics in Three Dimensional Geometry Class 12 for board exams?

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question