Why should I use chapter-wise NCERT Solutions for Class 12 3D Geometry provided by shiksha?

${\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left(\frac{x^{2}cosx}{1+{\pi }^2}+\frac{1+si{n}^{2}x}{1+e^{{\left(sinx\right)}^{2023}}}\right)dx}=\frac{\pi }{4}\left(\pi +\alpha \right)-2$

${\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left\{\left(\frac{x^{2}cosx}{1+{\pi }^x}+\frac{1+si{n}^{2}x}{1+e^{{\left(sinx\right)}^{2023}}}\right)+\left(\frac{x^{2}cosx}{1+{\pi }^{-x}}+\frac{1+si{n}^{2}x}{1+e^{-{\left(sinx\right)}^{2023}}}\right)\right\}dx}$

$=\frac{\pi }{4}\left(\pi +\alpha \right)-2$

${\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(x^{2}cosx+1+si{n}^{2}x\right)dx}=\frac{\pi }{4}\left(\pi +\alpha \right)-2$

${\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}{x}^{2}cosxdx}+{\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+si{n}^{2}x\right)dx}=\frac{\pi }{4}\left(\pi +\alpha \right)-2$ ....(1)

Let $I_1={\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+si{n}^{2}x\right)dx}$

$I_1={\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}1\cdot dx}+{\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(\frac{1-cos2x}{2}\right)dx}$

$I_1=\frac{\pi }{2}+\frac{1}{2}\left[\frac{\pi }{2}+0\right]$

$I_1=\frac{3\pi }{4}$

Let $I_2={\displaystyle \underset{0}{\overset{\frac{\pi }{2}}{\int }}{x}^{2}cosxdx}$

$I_2={\left[x^2\left(sinx\right)-{\displaystyle \int 2x}{\displaystyle \int cosxdx}\right]}_0^{\frac{\pi }{2}}$

$I_2={\left[x^2\left(sinx\right)-2{\displaystyle \int xsinx}\right]}_0^{\frac{\pi }{2}}$

$I_2={\left[x^{2}sinx-2\left(x\left(-cosx\right)+{\displaystyle \int cosx}\right)\right]}_0^{\frac{\pi }{2}}$

$I_2={\left[x^{2}sinx-2\left(-xcosx+sinx\right)\right]}_0^{\frac{\pi }{2}}$

$I_2=\left(\frac{{\pi }^2}{4}-2\right)$

Put l₁ and l₂ in (1)

$\frac{{\pi }^2}{4}-2+\frac{3\pi }{4}$

$\frac{{\pi }^2}{4}+\frac{3\pi }{4}-2$

$\frac{\pi }{4}\left(\pi +3\right)-2$

α = 3

Given $\left|\overrightarrow{a}\right|=1$ , $\left|\overrightarrow{b}\right|=4$ , $\overrightarrow{a}\cdot \overrightarrow{b}=2$

$\overrightarrow{c}=2\left(\overrightarrow{a}\times \overrightarrow{b}\right)-3\overrightarrow{b}$  

Dot product with  $\overrightarrow{a}$ on both sides

$\overrightarrow{c}\cdot \overrightarrow{a}=-6$ ... (1)

Dot product with  $\overrightarrow{b}$  on both sides

$\overrightarrow{b}\cdot \overrightarrow{c}=-48$ ... (2)

$\overrightarrow{c}\cdot \overrightarrow{c}=4{\left|\overrightarrow{a}\times \overrightarrow{b}\right|}^2+9{\left|\overrightarrow{b}\right|}^2$

${\left|\overrightarrow{c}\right|}^2=4\left[{\left|\overrightarrow{a}\right|}^2\cdot {\left|\overrightarrow{b}\right|}^2-{\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)}^2\right]+9{\left|\overrightarrow{b}\right|}^2$

${\left|\overrightarrow{c}\right|}^2=4\left[\left(1\right){\left(4\right)}^2-\left(4\right)\right]+9\left(16\right)$

${\left|\overrightarrow{c}\right|}^2=4\left[12\right]+144$

${\left|\overrightarrow{c}\right|}^2=48+144$

${\left|\overrightarrow{c}\right|}^2=192$

$cos\theta =\frac{\overrightarrow{b}\cdot \overrightarrow{c}}{\left|\overrightarrow{b}\right|\left|\overrightarrow{c}\right|}$

$cos\theta =\frac{-48}{\sqrt[]{192}\cdot 4}$

$cos\theta =\frac{-48}{8\sqrt[]{3}\cdot 4}$

$cos\theta =\frac{-3}{2\sqrt[]{3}}$

$cos\theta =\frac{-\sqrt[]{3}}{2}$ $\theta =co{s}^{-1}\left(\frac{-\sqrt[]{3}}{2}\right)$

(a – 1) × 2 + (b – 2) × 5 + (g – 3) × 1 = 0

2a + 5b + g – 15 = 0

Also, P lie on line

a + 1 = 2λ

b – 2 = 5λ

g – 4 = λ

2 (2λ – 1) + 5 (5λ + 2) + λ + 4 – 15 = 0

4λ + 25λ + λ – 2 + 10 + 4 – 15 = 0

30λ – 3 = 0

$\lambda =\frac{1}{10}$  

a + b + g = (2λ – 1) + (5λ + 2) + (λ + 4)

$=8\lambda +5=\frac{8}{10}+5=5.8$

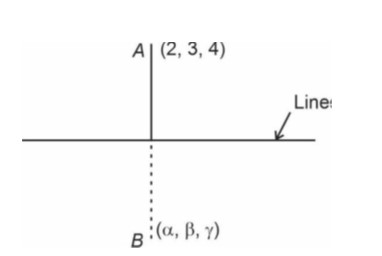
Take $\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda$  

x = 2λ + 1, y = 3λ + 2, z = 4λ + 3

  $\overrightarrow{AB}$  = (α − 2)  $\widehat{i}$ + (β − 3) $\widehat{j}$ + (γ − 4) $\widehat{k}$  

Now,

(α − 2) ⋅ 2 + (β − 3) ⋅3 + (γ − 4) ⋅ 4 = 0

2α − 4 + 3β − 9 + 4γ −16 = 0

⇒ 2α + 3β + 4γ = 29

$L_1=\frac{x-\lambda }{1}=\frac{y-\frac{1}{2}}{\frac{1}{2}}=\frac{z}{-\frac{1}{2}}$

$\therefore SD=\frac{\left|-2\lambda +3\left(2\lambda +\frac{1}{2}\right)+\lambda \right|}{\sqrt[]{14}}=\frac{\left|5\lambda +\frac{3}{2}\right|}{\sqrt[]{14}}$

$5\lambda +\frac{3}{2}=-\frac{7}{2}\Rightarrow 5\lambda =-5\Rightarrow \lambda =-1$

$\therefore \left|\lambda \right|=1$