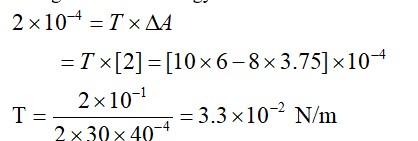12.17 Obtain the first Bohr's radius and the ground state energy of a muonic hydrogen atom [i.e., an atom in which a negatively charged muon (μ–) of mass about 207me orbits around a proton].
12.17 Obtain the first Bohr's radius and the ground state energy of a muonic hydrogen atom [i.e., an atom in which a negatively charged muon (μ–) of mass about 207me orbits around a proton].
12.17 Mass of a negatively charged muon, = 207
According to Bohr's model
Bohr radius,
And, energy of a ground state electronic hydrogen atom
Also, the energy of a ground state muonic hydrogen atom,
We have the value of the first Bohr orbit, = 0.53 Å = 0.53 m
Let be the radius o
Similar Questions for you
Kindly go through the solution
Change in surface energy = work done
|DE0| = –10.2
]
= 3 m/s
n = 4
Number of transitions =
Kinetic energy: Potential energy = 1 : –2
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics Ncert Solutions Class 12th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering