14.11 Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
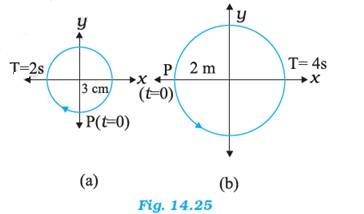
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
14.11 Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
(a) Time period, T = 2 s, Amplitude A = 3 cm
At time, t = 0, the radius vector makes an angle with the positive x-axis, i.e. phase angle = +
Therefore, the equation of simple harmonic motion for the x-projection of the radius vector, at time t is given by the displacement equation:
x = Acos = 3cos
Similar Questions for you
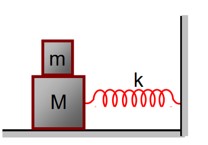
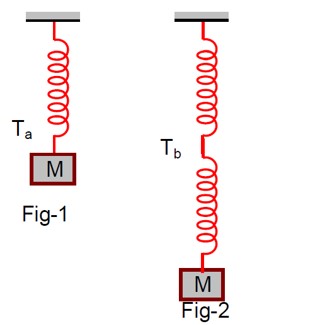
Velocity of block in equilibrium, in first case,
Velocity of block in equilibrium, is second case,
From conservation of momentum,
Mv = (M + m) v’
f? = 300 Hz
3rd overtone = 7f? = 2100 Hz
Kindly consider the following figure
K = U
½ mω² (A² - x²) = ½ mω²x²
A² - x² = x²
A² = 2x²
x = ± A/√2
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

physics ncert solutions class 11th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering