14.11 Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

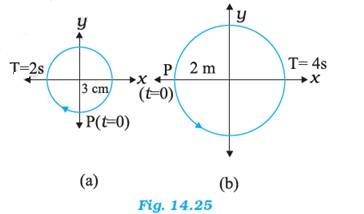
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.

If the time period of a two meter long simple pendulum is 2s, the acceleration due to gravity at the place where pendulum is executing S.H.M. is:

In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. New amplitude of oscillation will be:

The fundamental frequency of an organ pipe open at one end is 300 Hz. The frequency of 3rd overtone of n Find n.×this organ pipe is 100 Hz

Consider two identical springs each of spring constant k and negligible mass compared to the mass M as shown. Fig. 1 shows one of them and Fig. 2 shows their series combination. The ratios of time period of oscillation of the two SHM is T_b / T_a = √x, where value of x is ................... (Round off to the Nearest Integer)

For what value of displacement the kinetic energy and potential energy of a simple harmonic oscillation become equal?
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->