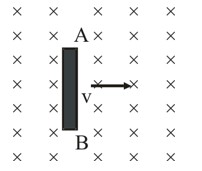
6.17 A line charge l per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.22). A uniform magnetic field extends over a circular region within the rim. It is given by,

B = – B₀ k  (r $\le$ a; a < R)

= 0 (otherwise)

What is the angular velocity of the wheel after the field is suddenly switched off?

A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure then :-

An aeroplane, with its wings spread 10m, is flying at a speed of 180 km/h in a horizontal direction. The total intensity of earth’s field at that part is 2.5 × 10^-4Wb/m² and the angle of dip is 60°. The emf induced between the tips of the plane wings will be…………..

Two conducting circular loops of radii R₁ and R₂ are placed in the same plane with their centres coinciding. If R₁ » R₂, the mutual inductance M between them will be directly proportional to:

A small bar magnet is moved through a coil at constant speed from one end to the other. Which of the following series of observations will be seen on the galvanometer G attached across the coil?

Three positions shown describe:

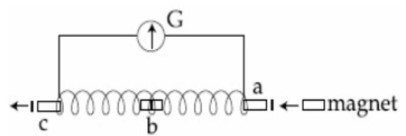
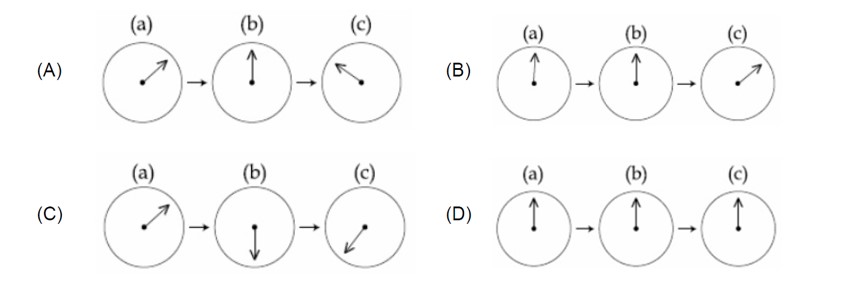
(a) the magnet's entry

(b) magnet is completely inside and

(c) magnet's exit

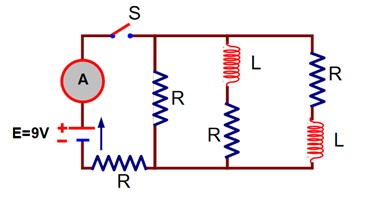
Figure shows a circuit that contains four identical resistors with resistance R = $2.0\Omega ,$ <!-- [if gte mso 9]><xml> </xml><![endif]--> two identical inductors with inductance L = 2.0mH and an ideal battery with emf E = 9V. The current ‘i’ just after switch ‘S’ is closed will be: