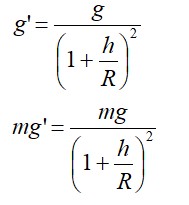8.2 Choose the correct alternative:
(a) Acceleration due to gravity increases/decreases with increasing altitude
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density)
(c) Acceleration due to gravity is independent of mass of the earth/mass of the body
(d) The formula –G Mm(1/r2
– 1/r1) is more/less accurate than the formula mg(r2
– r1) for the difference of potential energy between two points r2
and r1
distance away from the centre of the earth
8.2 Choose the correct alternative:
(a) Acceleration due to gravity increases/decreases with increasing altitude
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density)
(c) Acceleration due to gravity is independent of mass of the earth/mass of the body
(d) The formula –G Mm(1/r2 – 1/r1) is more/less accurate than the formula mg(r2 – r1) for the difference of potential energy between two points r2 and r1 distance away from the centre of the earth
-
1 Answer
-
(a) Decreases - Acceleration due to gravity at depth h is given by = (1 – )g, where g = acceleration due to gravity on the surface of the Earth. From this equation, it is clear that acceleration due to gravity decreases with increase in height
(b) Decreases – Acceleration due to gravity at depth d is given by = (1- )g. So the acceleration due to gravity decreases with increase in depth.
(c) Mass of the body – Acceleration due to gravity of body mass m is given by the relation g = , where G = Universal gravitation constant, M = mass of the Earth and R = radiu
...more
Similar Questions for you
->R3 = (R + x)2 (R – x)
->R3 = (R2– x2) (R + x)
->x2 + Rx – R2 = 0
Stress
R is not correct.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers