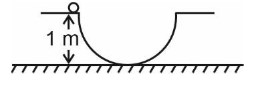
A ball is released from a height of 1 m on a smooth hemispherical surface as shown. Find its velocity when it is at a height of 0.5 m. (Take g = 10 m/s²)

 

From conservation of Energy:

$mg\mathcal{l}\left(1-cos60°\right)=\frac{1}{2}m{v}^2$

$\Rightarrow v^2=2g\mathcal{l}\left(\frac{1}{2}\right)=g\mathcal{l}$

$=10\times \frac{25}{10}=5m/s$

(1/2)kx² = (1/2)mv² ⇒ x = v√ (m/k) = 10 × √ (4/100) = 10 × (2/10) = 2m

Yes. Mechanical energy is the sum of both kinetic and potential energies. Kinetic energy cannot be a negative value since mass is always positive and velocity square leads to a positive value. However, potential energy can be negative depending on the reference point.

Conservation of Mechanical Energy is linked to newton's second law of motion (F = ma) in combination with work energy theorem. The work energy theorem states that total work done on an object equals to change in kinetic energy. This theorem is used to prove that the sum of kinetic energy and potential energy remains constant.