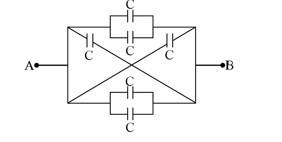
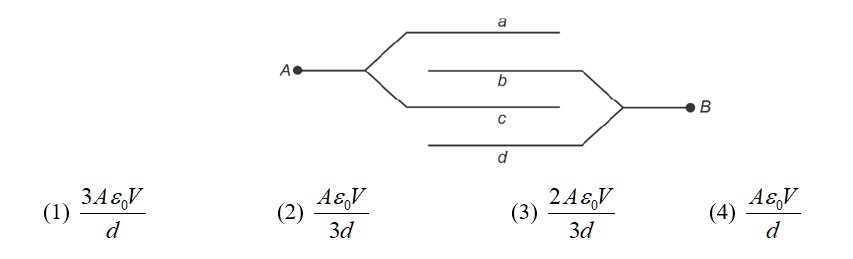
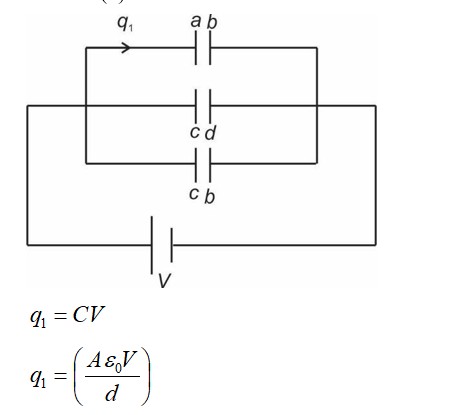
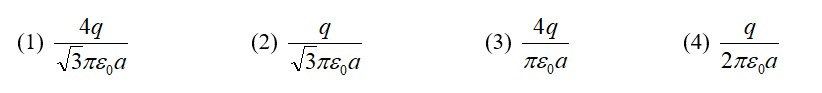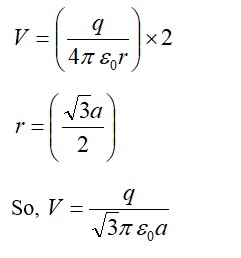A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as
ε(x) = ε? + kx, for 0 < x ≤ d/2
ε(x) = ε? + k(d-x), for d/2 ≤ x ≤ d
A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as
ε(x) = ε? + kx, for 0 < x ≤ d/2
ε(x) = ε? + k(d-x), for d/2 ≤ x ≤ d
dC? = (ε? + kx)A / dx [For 0 < x < d/2]
1/C? = ∫ dx / (ε? + kx)A) from 0 to d/2
= (1/Ak) [ln (ε? + kx)] from 0 to d/2
= (1/kA) ln (1 + kd/ (2ε? )
C? = kA / ln (1 + kd/ (2ε? )
Similarly dC? = (ε? + k (d-x)A / dx [For d/2 ≤ x ≤ d]
C? = kA / ln (1 + kd/ (2ε? )
Clearly, C? = C? = C
For series combination:
C_eq = C? / (C?
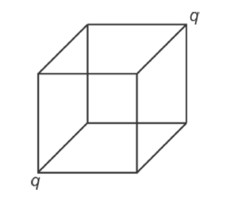
Similar Questions for you
Please find the answer below
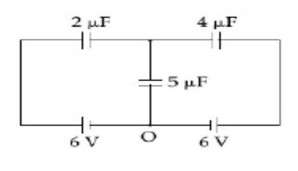
Now, using junction analysis
We can say, q? + q? + q? = 0
2 (x - 6) + 4 (x - 6) + 5 (x) = 0
x = 36/11, q? = 36 (5)/11 = 180/11
q? = 16.36µC
Capacitance of element
Capacitance of element,
Given:
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics Electrostatic Potential and Capacitance 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering