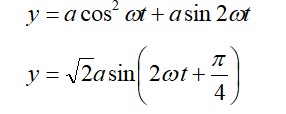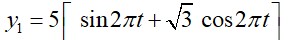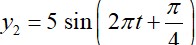A particle is making simple harmonic motion along the X-axis. If at a distances x1 and x2 from the mean position the velocities of the particle are
respectively. The time period of its oscillation is given as:
A particle is making simple harmonic motion along the X-axis. If at a distances x1 and x2 from the mean position the velocities of the particle are respectively. The time period of its oscillation is given as:
Option 1 -
T =
Option 2 -
Option 3 -
Option 4 -
-
1 Answer
-
Correct Option - 1
Detailed Solution:As we know that for SHM, so
Subtracting equation (ii) from equation (i), we have
Similar Questions for you
Then,
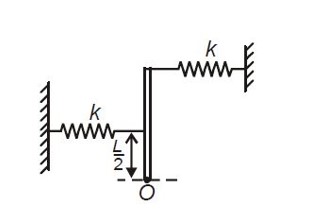
Given mg = kL
∴ Iα = (kLθ.L + k (L/2)²θ - mg (L/2)θ)
(mL²/3)α = kL² (3/4)θ (restoring torque)
α = (9k/4m)θ
∴ ω = (3/2)√ (k/m)
y = A sin (2πt/T)
t? - t? = (T/2π) [sin? ¹ (x? /A) - sin? ¹ (x? /A)]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers