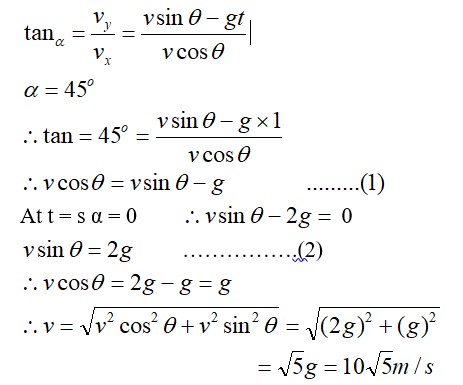A particle is moving in a circle of radius 1m with angular velocity (ω) given as a function of angular displacement ( θ ) by the relation ω = θ² + 2θ. The total acceleration of the particle when θ = 1rad is:
A particle is moving in a circle of radius 1m with angular velocity (ω) given as a function of angular displacement ( θ ) by the relation ω = θ² + 2θ. The total acceleration of the particle when θ = 1rad is:
ω = θ² + 2θ
α = (ωdω)/dθ = (θ² + 2θ) (2θ + 2)
At θ = 1rad.
ω = 3rad/s and α = 12rad/s²
a? = αR = 12 m/s² a? = ω²R = 9 m/s² A? = √ (a? ² + a? ²) = 15 m/s²
Similar Questions for you
Please find the solution below:
after 10 kicks,
v? = 3tî v? = 24cos 60°î + 24sin 60°? = 12î + 12√3?
v? = v? – v? = (12 – 3t)î + 12√3?
It is minimum when 12 - 3t = 0 ⇒ t = 4sec
a? = v? ²/4r
a_A? = (v? ²/r²) × r = v? ²/r
a_A = 3v? ²/4r
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics Motion in Plane 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering