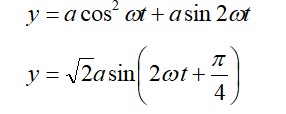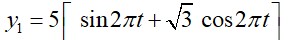A particle of mass 1 kg is hanging from a spring of force constant 100 Nm-1. The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period T. The time when the kinetic energy and potential energy of the system will become equal, is
The value of x is________.
A particle of mass 1 kg is hanging from a spring of force constant 100 Nm-1. The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period T. The time when the kinetic energy and potential energy of the system will become equal, is The value of x is________.
-
1 Answer
-
(Eq. of a particle executing SHM)
When KE = PE
A2 – x2 = x2
Similar Questions for you
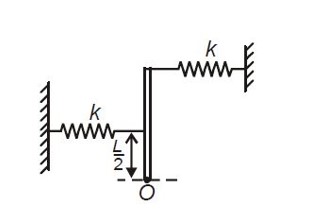
Then,
Given mg = kL
∴ Iα = (kLθ.L + k (L/2)²θ - mg (L/2)θ)
(mL²/3)α = kL² (3/4)θ (restoring torque)
α = (9k/4m)θ
∴ ω = (3/2)√ (k/m)
y = A sin (2πt/T)
t? - t? = (T/2π) [sin? ¹ (x? /A) - sin? ¹ (x? /A)]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers