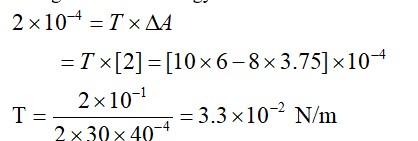A particle of mass m moves in a circular orbit in a central potential field U(r) = U₀r⁴. If Bohr's quantization conditions are applied, radii of possible orbitals rₙ vary with nᵃ, where α is---------.
A particle of mass m moves in a circular orbit in a central potential field U(r) = U₀r⁴. If Bohr's quantization conditions are applied, radii of possible orbitals rₙ vary with nᵃ, where α is---------.
-
1 Answer
-
From the given relations:
mv²/r = |dU/dr| = 4|U? |r³ . (1)
mvr = nh / 2π . (2)
By combining equations (1) and (2), we can derive the radius r:
r = ( (nh)² / (4π√* (U? )*) )¹/³ ⇒ r ∝ n²/³
Similar Questions for you
Kindly go through the solution
Change in surface energy = work done
|DE0| = –10.2
]
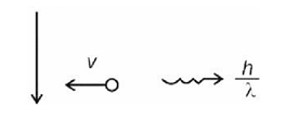
= 3 m/s
n = 4
Number of transitions =
Kinetic energy: Potential energy = 1 : –2
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers