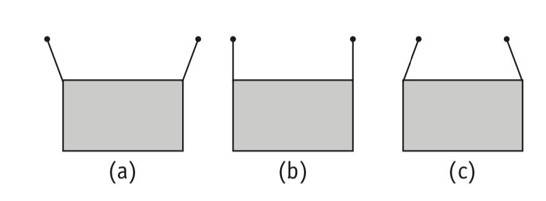
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Fig. 9.2). It can be done in one of the following three ways The tension in the strings will be
(a) The same in all cases
(b) Least in (a)
(c) Least in (b)
(d) Least in (c)
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Fig. 9.2). It can be done in one of the following three ways The tension in the strings will be
(a) The same in all cases
(b) Least in (a)
(c) Least in (b)
(d) Least in (c)

This is a multiple choice answer as classified in NCERT Exemplar
(c) 2Tsin -mg=0
2Tsin =mg
Total horizontal forces = Tcos
T=mg/2sin
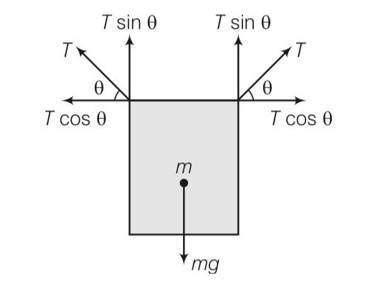
As mg is constant T
Tmax= mg/sin min
Sin min=0, min= 0
Tmin=mg/2sin max
max= 1, =900
Similar Questions for you
If is Poisson’s ratio,
Y = 3K (1 - 2 ) ……… (1)
and Y = 2 ……… (2)
With the help of equations (1) and (2), we can write
dm = (m/L)dx
∴ T = (mω²/2L) (L² - x²)
∴ ΔL = ∫? (mω²/2Lπr²Y) (L² - x²)dx
= ΔL = mω²L²/3πr²Y
Initially S? L = 2m
S? L = √2² + (3/2)²
S? L = 5/2 = 2.5 m
? x = S? L - S? L = 0.5 m
So since λ = 1 m. ∴? x = λ/2
So white listener moves away from S? Then? x (= S? L − S? L) increases and hence, at? x = λ first maxima will appear.? x = λ = S? L − S? L.
1 = d - 2 ⇒ d = 3 m.
Loss in elastic potential energy = Gain in KE
½ (YA/L)x² = ½mv²
0.5 × (0.5×10? × 10? / 0.1) × (0.04)² = 20×10? ³ v²
0.5 × (5×10²) × 1.6×10? ³ = 20×10? ³ v²
0.4 = 20×10? ³ v²
v² = 20 => v = √20 ≈ 4.47 m/s
(Re-checking calculations)
0.5 * ( (0.5e9 * 1e-6) / 0.1) * (0.04)^2 = 0.5 * (5e2) * 1.6e-3 = 4.
0.5 * 2
As we know that
If length and diameter both are doubled
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics NCERT Exemplar Solutions Class 11th Chapter Nine 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering
