A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become:

$\overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}$

= $\left(3\widehat{i}-\widehat{j}\right)\times \left(3\widehat{j}+\widehat{k}\right)$

$=9\widehat{k}+3\left(-\widehat{j}\right)-\widehat{i}$

$=-\widehat{i}-3\widehat{j}+9\widehat{k}$

$\left|\overrightarrow{L}\right|=\sqrt[]{1+9+81}=\sqrt[]{91}$

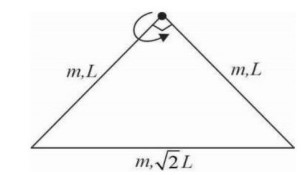
L = Iω
I = (mL²/3) + (mL²/3) + [m (√2L)²/12] + m (L/√2)² = mL² [2/3 + 1/6 + 1/2] = (4mL²/3); L = (4/3)mL²ω

Yes, an object moving in a straight path can also possess angular momentum with respect to a referenc epoint which doesn't lie on it's path. In such cases. the referenc epoint may lie perpendicular distance from the axis. If an object is moving in a straight line (not through the reference point) the perpendicular distance $r_\perp$ (l = rp) will be non-zero.

Yes, how much time these planets take in completing an orbit around the sun hugely depends on their distance from the sun as well as their mass. Since these planets move in a circular orbit, the term angular momentum is used in such cases for computing relevant information.

Angular momentum also depends on how the mass is spread over the body and not just mass only. If you closely look at the formula of angular momentum:

L=r*p

You will observe that it is a cross product of two vector quantities. Hence, the formula won't be practical without direction being involved.