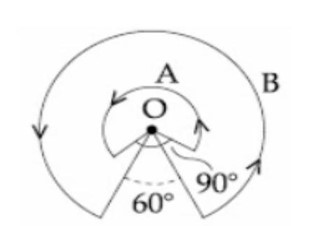
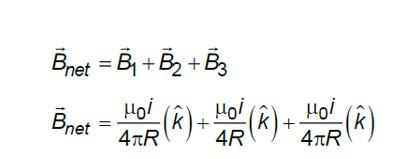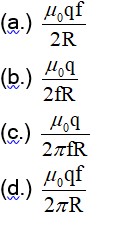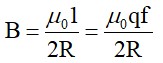A wire A, bent in the shape of an arc of a circle, carrying a current of 2 A and having radius 2 cm and another wire B, also bent in the shape of arc of a circle, carrying a current of 3 A and having radius of 4 cm, are placed as shown in the figure. The ratio of the magnetic fields due to the wires A and B at the common centre O is:

 

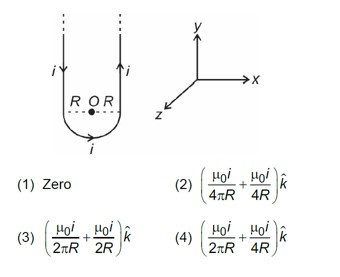
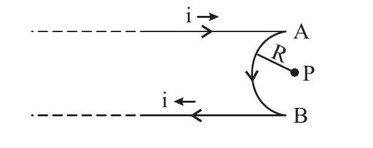
If currents are flowing in same direction, magnetic field will cancel each other, so the currents must flowing in opposite direction

$B_P=\frac{{\mu }_{0}I}{2\pi r}\times 2$

$\Rightarrow 300\times 10^{-6}=\frac{4\pi \times 10^{-7}}{2\pi \times 4\times 10^{-2}}\times 2$                                                                           

$\Rightarrow$ I = 30 A

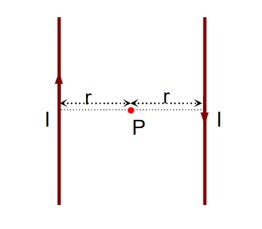
When the ring rotates about its axis with a uniform frequency fHz, the current flowing in the ring is

I=q/T=qf

Magnetic field at the centre of the ring is

for $\pi R^{2}Area\to \text{'}l\text{'}$ current\

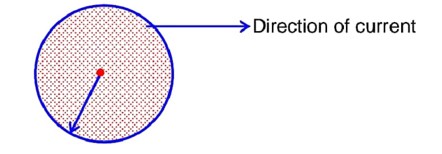
1 unit Area ® $\frac{l}{\pi R^2}$  

              $\pi r^2\to \frac{l}{\pi R^2}\times \pi r^2$  

$i=\frac{l{r}^2}{R^2}$              

 

Now, consider Amperian loop of radius small ‘r’ ln Amperian loop magnetic field will be tangential to the amperian loop.

${\displaystyle ?\overrightarrow{B}.d\overrightarrow{i}={\mu }_0{l}_{enclosed}}$           (Ampere circuital law)

$B=\frac{{\mu }_0}{2\pi }\frac{l}{R^2}r$

$B\propto r$  

${\stackrel{?}{\mathrm{B}}}_{\mathrm{P}}={\stackrel{?}{\mathrm{B}}}_{\text{upper wire}}\otimes +{\stackrel{?}{\mathrm{B}}}_{\text{semi-circle}}?+{\stackrel{?}{\mathrm{B}}}_{\text{lower-wire}}\otimes$

$B_P=-\frac{{\mu }_{0}i}{4\pi R}+\frac{{\mu }_{0}i}{4R}-\frac{{\mu }_{0}i}{4\pi R}=\frac{{\mu }_0\mathrm{i}}{4\mathrm{R}}\left(1-\frac{2}{\pi }\right)$ pointing away from the page