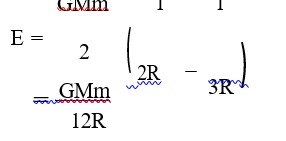In free space, two particles of mass m each are initially both at rest at a distance a from each other. They start moving towards each other due to their mutual gravitational attraction. The time after which the distance between them has reduced to a/2 is

Option 1 -

( (π+2) / 4√2 ) (a³/Gm)¹/²

Option 2 -

( (π-2) / 4√2 ) (a³/Gm)¹/²

Option 3 -

( (π+2) / 8 ) (a³/Gm)¹/²

Option 4 -

( (π-2) / 8 ) (a³/Gm)¹/²

2 Views | Posted 3 weeks ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

3 weeks ago

Correct Option - 3

Detailed Solution:

Let the origin be at the CM of the particles, let the initial positions of the particles be x = a/2 and x = -a/2 and let the instantaneous positions of the particles be x = r and x = -r
Let the instantaneous velocity of each particle be v
Let the time after which the distance between the particles has reduced to a/2 be T
Then, for the particle that was initially at x = -a/2,
(Gm²/ (2r)²) = -m (vdv/dr) ⇒ (Gm/r²) = - (4vdv/dr) ⇒ -4∫vdv = Gm∫ (dr/r²)
[v is negative because the velocity is towards the –X direction]
dr/dt = -√ (Gm/2) (1/r - 2/a)¹? ²
⇒ ∫ (a/2)^ (a/4) (r/√

...more

0 Upvotes 0 Downvotes

Similar Questions for you

A wire can be broken by a load of 20 kg-wt. The force required to break wire of same material with twice the diameter will be

alok kumar singh

The radii of circular orbits of two satellites A and B of the earth, are 4R and R, respectively. If speed of satellite A is 2V, then the speed of satellite B will be

alok kumar singh

At a point away from planet of radius 6400 km, the gravitational potential and field are –6.4 × 10⁷ SI units and 6.4 SI units respectively. Find height of that point above surface of planet.

alok kumar singh

$\frac{G M}{r} = 6.4 * 1 0^{7}$ . (i)

$\frac{G M}{r^{2}} = 6.4$ . (ii)

$r = \frac{6.4 * 1 0^{7}}{6.4}$

= 10⁷ m

= 10,000 km

R + h = 10,000

h = 10,000 – 6400 = 3600 km

Mass of moon is $\frac{1}{81}$ times the mass of a planet and radius is $\frac{1}{9}$ times the radius of the planet. The ratio of escape speed from planet to escape speed from moon is ________.

alok kumar singh

-> $V_{e s c} = \sqrt[]{\frac{2 G M}{R}}$

$R a t i o = \sqrt[]{\frac{81}{9}} = 3$

If the gravitational acceleration at the surface of earth is g, then increase in potential energy in lifting an object of mass m from earth surface to a height equal to half of radius of earth from surface will be:

alok kumar singh