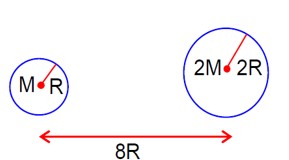
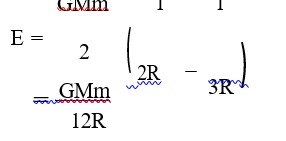Overview Physics Gravitation Physics Class 11th

Suppose two planets (spherical in shape) of radii R and 2R, but mass M and 9M respectively have a centre to centre separation 8R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √(aGM/(7R)) then the value of 'a' is _______. [Given: The two planets are fixed in their position]

2 Views | Posted a month ago

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

a month ago

We have to find the point where the gravitational field must be zero.
EG = 0
GM/x² = G (9M)/ (8R-x)²
1/x² = 9/ (8R-x)²
8R - x = 3x => x = 2R
Potential at A (surface of first planet), VA = -GM/R - G (9M)/7R = -16GM/7R
Potential at point x, Vx = -GM/x - G (9M)/ (8R-x) = -GM/2R - G (9M)/6R = -2GM/R
ΔV = Vx - VA = -2GM/R - (-16GM/7R) = (-14+16)GM/7R = 2GM/7R
Using conservation of mechanical energy
ΔKE = ΔU = mΔV
½mv² = m (2GM/7R)
v² = 4GM/7R
v = √ (4GM/7R) => a = 4

0 Upvotes 0 Downvotes

Similar Questions for you

A wire can be broken by a load of 20 kg-wt. The force required to break wire of same material with twice the diameter will be

alok kumar singh

The radii of circular orbits of two satellites A and B of the earth, are 4R and R, respectively. If speed of satellite A is 2V, then the speed of satellite B will be

alok kumar singh

At a point away from planet of radius 6400 km, the gravitational potential and field are –6.4 × 10⁷ SI units and 6.4 SI units respectively. Find height of that point above surface of planet.

alok kumar singh

$\frac{G M}{r} = 6.4 * 1 0^{7}$ . (i)

$\frac{G M}{r^{2}} = 6.4$ . (ii)

$r = \frac{6.4 * 1 0^{7}}{6.4}$

= 10⁷ m

= 10,000 km

R + h = 10,000

h = 10,000 – 6400 = 3600 km

Mass of moon is $\frac{1}{81}$ times the mass of a planet and radius is $\frac{1}{9}$ times the radius of the planet. The ratio of escape speed from planet to escape speed from moon is ________.

alok kumar singh

-> $V_{e s c} = \sqrt[]{\frac{2 G M}{R}}$

$R a t i o = \sqrt[]{\frac{81}{9}} = 3$

If the gravitational acceleration at the surface of earth is g, then increase in potential energy in lifting an object of mass m from earth surface to a height equal to half of radius of earth from surface will be:

alok kumar singh