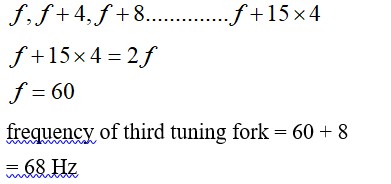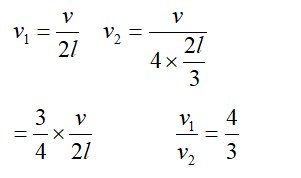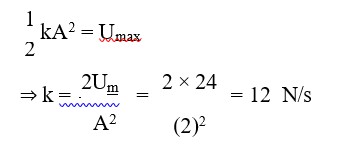The displacement of a string is given by y(x,t) = 0.06 sin (2πx/3) cos (120πt) where x and y are in m and t in s. The length of the string is 1.5m and its mass is 3.0×
.
(a) It represents a progressive wave of frequency 60Hz.
(b) It represents a stationary wave of frequency 60Hz.
(c) It is the result of superposition of two waves of wavelength 3 m, frequency 60Hz each travelling with a speed of 180 m/s in opposite direction.
(d) Amplitude of this wave is constant.
The displacement of a string is given by y(x,t) = 0.06 sin (2πx/3) cos (120πt) where x and y are in m and t in s. The length of the string is 1.5m and its mass is 3.0× .
(a) It represents a progressive wave of frequency 60Hz.
(b) It represents a stationary wave of frequency 60Hz.
(c) It is the result of superposition of two waves of wavelength 3 m, frequency 60Hz each travelling with a speed of 180 m/s in opposite direction.
(d) Amplitude of this wave is constant.
-
1 Answer
-
This is a multiple choice answer as classified in NCERT Exemplar
(b, c) y (x, t) = 0.06 sin (2πx/3) cos (120πt)
(a) y (x, t)=asinkxcoswt
(b) w=120 , f=60hz
(c) k=2 , v =60 (3)=180m/s
(d) since in stationary wave all particles of the medium executes SHM with varying amplitude nodes.
Similar Questions for you
The acceleration of wave is g/2. Its speed increases as it moves up. So answer is (2)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers