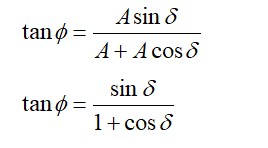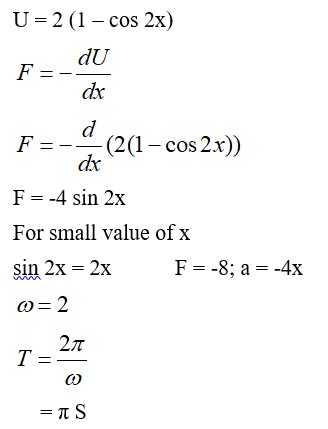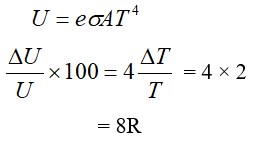The displacement vector of a particle of mass m is given by r(t)=ȋ A cos ĵ B sinwt.
(a) Show that the trajectory is an ellipse.
(b) Show that F= -mw2/r
The displacement vector of a particle of mass m is given by r(t)=ȋ A cos ĵ B sinwt.
(a) Show that the trajectory is an ellipse.
(b) Show that F= -mw2/r
3 Views|Posted 6 months ago
Asked by Shiksha User
1 Answer
A
Answered by
6 months ago
This is a Long Answer type Questions as classified in NCERT Exemplar
Explanation- displacement vector of particle is r (t)=? Acos ? Bsinwt
X=Acoswt
x/A= coswt………1
displacement along y axis is
y=Bsinwt
y/B= sinwt……….2
squaring and then adding eqn1 and 2 we get
x2/A2+y2/B2=cos2wt+sin2wt =1
this is an equati
Similar Questions for you
From A to B the process is isobaric
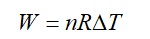
= W = 2 × R (600 - 350)
= 500 R
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
66K
Colleges
|
1.2K
Exams
|
6.8L
Reviews
|
1.8M
Answers
Learn more about...

Physics NCERT Exemplar Solutions Class 11th Chapter Five 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
or
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
or
See what others like you are asking & answering