The transverse displacement of a string (clamped at its both ends) is given by y (x,t) = 0.06 sin (2πx/3) cos (120πt). All the points on the string between two consecutive nodes vibrate with
(a) Same frequency
(b) Same phase
(c) Same energy
(d) Different amplitude.
The transverse displacement of a string (clamped at its both ends) is given by y (x,t) = 0.06 sin (2πx/3) cos (120πt). All the points on the string between two consecutive nodes vibrate with
(a) Same frequency
(b) Same phase
(c) Same energy
(d) Different amplitude.
-
1 Answer
-
This is a multiple choice answer as classified in NCERT Exemplar
(a, b, d) As we know by y (x, t) = 0.06 sin (2πx/3) cos (120πt)
By comparing the equation with general equation N denotes nodes and A denotes antinodes.
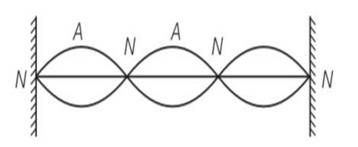
(a) Clearly frequency is common for all the points
(b) Consider all the particles between two nodes they are having same phase at given time
(c) But are having different amplitude of 0.06sin (2 ) and because of different amplitudes they are having different energies.
Similar Questions for you
The acceleration of wave is g/2. Its speed increases as it moves up. So answer is (2)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers