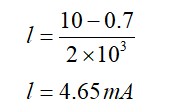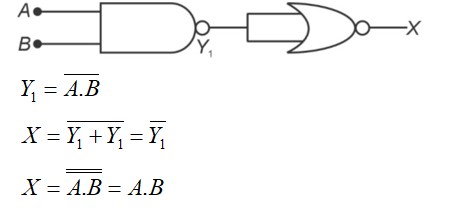The truth table for the following, logic circuit is
The truth table for the following, logic circuit is
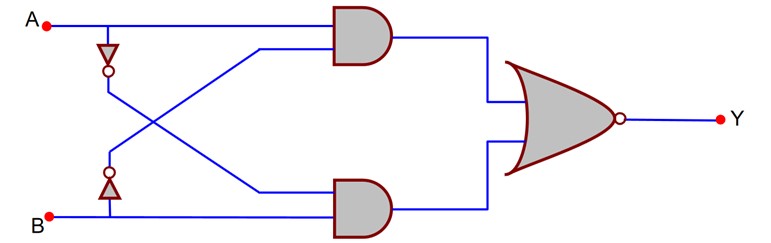
Option 1 - <p>Image 1</p>
<p><img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAL4AAACUCAYAAAAtQ5PNAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFiUAABYlAUlSJPAAAByASURBVHhe7Z0HWBRH/8e/9N5BFBG7oEmsYNcgIIolr71QxMRekmhM/rHFkhhjEo2JiXljXmNDsQEWbBEUiICoUewFOyIqvfe7+e/srcFyiCZgbnb38zz77PK7vedhbn4zOzs3+zktwgEZGYmhLexlZCSFnPgykkROfBlJIie+jCSRE19GklQ5q6NUKlFSUgKFQsFvYkBLS+uvTSxlehm0tbX5jVa1lMr9JLT8enp6MDIy4v+uMvFTU1MxduxYpKWloby8nP/QWIb+/2ZmZjA0NISuri4ePHjANwApYGFhwZeddmQZGRlCVDo87uicnJywf/9+vgFUmfhZWVkYOHAgPDw8+I31xKfo6OjwLZ9CG7NUKC4uxrfffov+/fvD1dVVFHX5KtDEP3XqFLZs2YKEhARVr08TXx35+fnE3d2dhIWFCREZViktLSXdunUj4eHhQkR6xMXFkbZt25KCggL+7ypvbrnX+D29PMqwTWFhId/rlZWVCRHpQa96Tw5tX8+sjiIf50/F4o8//sCN9EIhyBb5D6/jGPf/0zI8ux07dhyXbj0UzhQHhQ+vIfpoNFe+E0h/ib4v4+4l7twoHEu8hlIWRlJ8v6+GvLw8fqgTHBwsRP4+aTGrSH0t0I+DdHo/iJQLcZY4sSaQ//+r2vTtXcjw978lZx5oXum4+zXSvXt3EhoaKkSqJ/vKTtLRTFW2wYv3EYUQV0dF+mni+4Y1f27/hTtJgVJ4QYOIjIwk7dq1q36oU3OU41D4fjzgPhZ97m76/J5NOJ5GPyO20NbR4y+PJo5vwaf/AP5GkW4D+vvAo0dX1K+4jp0/foKRkxbhdrHqPSxj6TIMP3w7BQbc8a5Vc7H9TJbqheeoQMiK2Qi+lAXHbh9g5exhMGFhsoxPfzXUVI+vyEokQ1oYE/MWnmRSoDeX8QZkxsazwqvscGrtBL5H6/DBOiHyNGmX9pJ+LU24c/TI9PWJQlQz+Ds9Pk/JfbJgYDO+3E0GLiQP1VzM0k6sIS5G3JXBvCVZdzJdiGoer73Hv52wH5FJRXByD8QHvr1hjVKE7AjFI0a/R1EqKrhr2PPYtRqImeMGQIt7NfbQEeQJcaYxcMDMJV+inS1wK3w5lm09I7wgUHoHX83/EleLtTBy9vcY68adyAi1nPjFOLxjB5cEOnB374RW3fugq5M+UqLCEH05VziHMQjhB77qsGvQBHrcvqggF2KZC7NsPRzfzvGDMQrx68IFiE4tFV4BYtYswM8RybDv9T6++tCba/TsUKuJr3yYgJ0HzwPmHTGgayPA+E2MGNiWy4xL2BB6TDiLMbS0qvzQUq5eBJ0wbPRWO7DT91WHFjynfoGJnk4our0fi77ezl/xlMkRmPdVEEoNWmLZ15+hsbHqbFao1cRPPLAbxx8Bzb0HwM1Rn4toocd/hnDDHSA2bBsuMjizqaWtA13huJISJO7/CUt+PQBdu86YGOhZ25fS14thY8z96jO0MuJ6+d++w95zNxG0YiHiHupiyMJv4M/QEOcxtVc/JAsHDx7iUsII/fv3g7WOKtywQ194u+ig4OJBhEbcUgVZgLuO04S/um0x2rVvj/ZPbB3adEDvYe8jIacVvgkOw1AXc9V7RISd23tY8nF/6BSew4zRwzFn9XE4dpuCZTMHqOkINJ9aS/yiG8cRHpkEfYfOGESHNwJa1m0wZGgf6HANY+/evSioasCsgdAxbFF6Ms4mJiLxie3M+cvIpIN6RRZOR4bicoYY1wFpY9CsrzC2Uz2kXEnEA/PW+HzlZ2huKLzMGLWW+IkRO3AqB7Bv1R4WOTdx48YNYbuFuo1b8VeAM+HcUOgeI7eBXAOt4HYths1DwunTOP3EdurEcUSGrMHQN8qw5ev34TdlGe4y8fXlq6Fl8RZGDvHgO4DmfUZjsJud6gUGqZ3EV6Ri1/YIfvbjXuQKtGvWDM2bNxe2pug5fjnS6XRmRjyCDyTyb2EBWh5zxxbo9MxQx7VjZ3gOnYiNW/4H9/oGOBvyI7Ydual6k8gw0KPzVoCxkR7fAFilVhI/58wB7P6Tu6s1b4R3RvpjjL8/fH19hc0PY8aMwcBuztyZ5TgYtA33GOocFWUl/MyNOkyc3eHt1ow7SkfSzRRVUGQolEp+r1QooTpik1pIfAWiwvfhZpES7Yd+gM3bgrAxKIhfC63aNmPjxo0I+nkR2hoDjxL3YE+cWB6OUKCknA6I6Nr/WhtFytQANV87+ddx4FAEd2DJr2UxU0Wfw+JNd/TzaAgUJyN8z+9V9qKahq6hMejErDoeHg/D/gQ6xHHCW60aq4IyGkmNJ/6904ew71QRDBp3gY97CyGqBu26GDigH+gyj6O7wpD4SPNnQuiYNv1iLLaHhiE0NFTYuOMd27Huu3kYOnI6TmdWoPngsRjUqYHqTTIaSc0mPinG7rU/g65Md/EaCTcbVbgqXPu9g9YWQMXNMKzde7rKpQCaQEVZAf//3Tm8BqOGDcWwYcOEjTseOQrjZi1FfIo22vhMxbpVs9FA9Uyz6CgvVn0OOQXFGl1f1VGzia/Igk69HvDz88PsCX2q/WJDt0EP/N+cGdz5o2BDCjX6Zsm+lSfGcOXy427QR48e/fTmG4DJMxdge0Q8YveuRndHkWY9h2N7b/jTz8G7A79kmVn4NZpqqMkHUWT+Xf72smQR8S88iCIjo3nIiS8jSapNfOqikWEbXqCkpSXpuqQSsSepUiiVn5+PAQMGICAgAEOHDhWibEMr//EmJZVebm4ufxM+depUvk6lCLVhLFy4EHFxcTAxMak68bmbAAQGBuL69euoqKj4y7PDMlSjZ2BgwPeAVCEoFczNzXlzHO31aL2KoS5fBdrR0Xq3tbXFvn37+OMX9vjUnUmVc126dBGi7EKLSSuefggUmgiPj8UOlSmtXLkSffv25RfVSZFLly5h9+7dCA8P5/2pL5zO7NGjBwkJCREiMqwiKwQJiY2NJa1bt3656Ux6MyRl7ZxYkBWCKhXmkzf3tT6dmXn3EmKijuJoVDTOXEsVomzz8MZZoUwxuHAzXYhKh5Rzx3Dq0h21mhVWqMXEz8GuHz6EVzc3uHt4wtOjFzp06gnf2T/iZoFwCmsoHmLjFxPg3sVVKJM7OnT1wISlm3BfIp1p8a19GNajJ0bM34h8IcYitZT4FYj44SMMn7EK17RbY+7ytdjw0+fo45SJrV9/gPGzfkE2c08xlGDnoqkYu2AtHth5YPGq9fjf8rnoZHoLa+cFYtKibag0zoiT0vt/YOp7U3GCy3hLC2Omn8CqlbU6BUmhpJ0JCBr0JAeu5wpRQhTpieQ9N1sC2JOvfr8lRNkg89Ra0lAHxLDFYBL3sFSIElJ0L4oMoOpA3Ubkl4Q0IapZ1MRanVuxO8mQdnZ0BpDfXMd+Q7KE11jgNazVUSB66xYkFgIDxs2CT7NK1Ya2bVvMnT8JhniEjZsOMtRDVuDQpnW4q9DBqBkfo6t95aMoRo7umP+RH3Qr7iB4y2H+gXRRUZSK3xaNhbvXcIQl5qFp0wb8gzgKxr8KqPnEV6Yj/s8/AS17ePTsKAQradjeC10sgBuxkewIpcrvICbuMqDnjN6dWwnBSt7q5AEXI+DsiSjcFNnvaCivHsQnizci2bAV5qwPx4bFvjDh4mWMf/Fd84mfm4E7d1MAMxs0qm8vBCvRtaiPRi10UJF+CUm3GbkjTE/BtfQcoF4DONWxFIKVGNs7wsEByEu+juQH4urzy40dMHHRSkQfj8bSsb1RV18pinuZGk/8isJcZKcroW1qD2tzNbc/hoawsOSSp7gI2blsTO+U5GQiNxcwsLKCKe3unsXEHHZmxlyjL0Bevri6fAMXHyxbOANvu6gcOiUVSrZvagVqPPFLijKQk00fyrZUnyR6BrA04xKfFCMrmw1jckFeHgrzufG8qSmM1D12ZGQMK2MzrvC5yMhnda5WWtR44lN/fAW92msRvHgtlBJlZWwMC5QKBZTV3MwRuu6HKFDGF15G06nxxDcytuWGMtxdf3m5qgE8S1kpNyLI4xqGEWys2ZCrmppbwJi7elWUlUHtaubiQuQUcZcEAwvUMTcVgjKaTI0nvq6xBSxtucQvTEWWupEMl/h5edxYSN8QlhZsJL6huTlMuZFMATeGy1c3E0XvVwqLuBZiCgtTxkTxEqXGE1/LwgoO9a2B/GykZavJkuI8ZKVylwIzBzg6sGEj0LathwbW3P+anons/OfnNJRcQ87OJNCxrwM7u6p0UzKaRI0nPvTt0cb5Da5nf4AzF64LwUqyks/iz2TAxrkL3nh+tlMzMWkMN+cGQM5lnEm6LwQrSb52DkmZQFNnNzR5frZTRgOp+cSHITwG9IEVShEWvAF3n1rCV44969fjHnfkObw/6qqCDGAGn+F9oYMcBK3bBi7HnyAHWzdv4WI68PqPD1duGRaohcQHGnkEYJynI+4f/gEBE75A/IU7SL15DusXBWLm6lhYOY/ErJGdhbPZoNWAyRjTxgpXQ+fD/4Mf8Oe1FNy7ehKrZo3B/OCLsO80Du8PbiOcLaPx8Ct21PBPhVK5tw8T/7ebqBY1GViROha6/LF5i54k6GSqcBZbpF0MI+90cODLoW1iS2yMVQu27NsPJLuu5AhnaR41KZQ6u34yX+b6gxaTTCHGAq9NKGXeqDeCwqMR9t/F8HvHA929BmPGl2sRF3MI/m71hLPYwu6NwQj9PQabV87BSJ+ecO83EnNWBCM2YhcGuVgIZ4kbG+eeGB8QgIA+rrJCUEazkRWCskJQRoZHTnwZSVJt4ssKQfaRFYJ/QyHo7++PwYMHC1G20dbW5hOAbtQOJxW4+zX+h/eoQrBfv35CVFrExsZi0aJFL68QTEpK4q1jVZzGFFQhSC1atPVLTSFIXaG0x6cdmhjq8lWgHR2tdzs7u5dXCLq5uaFr165ClF1oMaWsEFyxYgV8fHzQoUMHISotLl68iF27dskKQSkhKwRlhaAkkRWCeP0KwYw7FxF9JBKRR47i9NXnVzayjDL/ARL+iEZyjgRc+0WPcDo+GpGRkYg5fhYZjD9xXouJn42Q76bDo6sbenn1Rm8vT7h26oGRn3yPGyy75/6iDNuX+KPr272w43yREBMnt49vw4i+7nDt1gu9e/eGe9cO8PDxw9b428IZ7FFLiV+Ow99/hFGzVuOmfjvM+24dNq5egr6NcrBj+UyMn/VfBhWCT8KV75cZ+HDlURA9OxjrivcmOf/KPrw7egx2HkvBwCkLELR5PT4JdMe1qGAE+I/FviuMPlzPj/TV8I8UgtdCSVu6crHB2+TgjTwhSogy4ywZ35Fq6OqQpYduClHGKLhLNi8cRagngn58MKlLVsflCy9qJn97rU5FFlk+uiVXTgMS8H0EUQphQkrI/m9HET2u/C39vyM5FUJYg3ktCsGobVtwlrv6Dxz/Efo2NRPigJZNG8yeNwlGSMOmoINgy0CjxN2T2zC6Ty/4L96GYptmcLLV5YrL9KXrheQmRSF4zxUYNR+Aj8Z5PeHTMUC/Dz7DkGb6uBKyFbF32Rvq1XziK9Jx/JRKIdirh3qFYGdBIXiJqatkCfatWYptcbfQ/p2PsO9QCEa15fq8EvF+A5x8/hTo7UvzHn3x5rPyCP2W6Ovdkit/Iv44nSwE2aHmE58qBJOpQtC2CoWgg6AQvIykOwxNrxEFGnf1wzebjyAydAW8XBuhrETcYvCUW9d4CW6Tlo3w9EoXihYaN+cSnzvj7JUbqhBD1HjiVyoE67xAIWglKAQZmt7RMkO/cZ/iEz8PWNEsKCnmBvji/uY3LV31CzZ1bWz5/bOYW6m0gukZOfyeJWo88V9OIciNdXiFYJ4QlNE8lNzFW/UzRxZm6v1HhqaWfAIVpmWCFfH1Y2o88ZXKCijo9VFECkGpohBWsJIqK1J1zVNSw5wqwAw1nvhUIWjOjWTEpBCUJtqwsKnDH5VXqP+Zt5L8HK77AkzsbXhnPkvUeOLrGlvCyoZL/MJUZIpEIShVbISx/cOMNH7/LAV5OfyXGVY2VmDtEZcaT3wtC0vUExSC6dlq5iuLcwWFYH1mFIJSxcGpKb+/n5rB758lPU219qpZQ0d+zxI1nviVCsFUnLnw/DRXVvI5nKIKQReGFIISxbHlW3Di9tfiT+CRKvQEmTgVd57b14dr64aqEEPUfOL/pRAsQ+iW9bjzjEJw97p1SOGOvJhSCEqTum++Da/25nh0PBRbop/+ce5HcZuxNSYThm184PmmalqTJWoh8alCcAzGezVAasQqBIxfjLjzt3H/RiJ+WxCAmT/HwdplFGaN6CScLaOpaJm5YPK0sTAov4m5EwPwc/hxbthzD3HhP2H0uHm4C0vMmD0NzUwY/D6DX7Gjhn8qlMq7E0ECejVVLeTSsyR2Zjr8sYWzO9l86oFwFsMU3Sfj3+Lv7ciKmMqFeJrIPxJKlWeRjQtHE2ttVVnt7KxVdaptTUZ9sZVo9vK8Sl6bUMqsoRc27Y3G7l+XIHBYH/TqNwIfL1uPuJiD8HMVwSBH1wQeo8fh3Xeno62DiJ34ulYYsygYsVE7MGfaGPTq5YXAqXMQGp2ArfNHgdnff+HTXw2yQlA8yApBWSEoI8MjJ76MJKk28Z9Vr8mwx2OFoJTr8pUVgn5+fqJTCFKoWUwqUIUgrccpU6ZIWiG4ePHil1MIUpPa1atXeeuYGKAKQaqPoz2gVBWCtBFIESMjo1dTCHbs2BHdunV7wdJUdqAVT3t8uomlMb8MVCG4fPlyvrd3dXUVRV2+CrS+L1y4gNDQUD7xZYWgRJAVgrJCUJLICkG8foXgX5RkIOFING5lsG8dS006jSMRhxERcQRnrz+/blGUFD3En7FHcfhwBKLiziCdLTfMc7y2xP/9h0no5tUL6+MY9mdWPMBvC8aiZ2c3eHn3gbe3F1y7uGPs4nW4x3givIhbcVsx3Nsdbj080aePNzy6u8Kjry+C42SF4AsgOBn0KaYsDoMSVjDWY/XnaEqwfeFkjP9iIzLr98GS1Zuw/vvP0N06BRsXjcPERcGMCbJejvzLe/Gu7xiExKXiP1MXYfOWDfh0rCeSYrYiwH8Mwq8wKkLlR/pqqJG1OqWPyM6l44iDrmplH2BHlu5nUx2YcWINaaANYuQyjCSklQtRQkruHyP/ecOUQMeJrI5/JEQ1i7+vEMwk34xy4erNkASuOvKEQrCUHFrhS/S5OnX2XU6yKz8OjeW1rdVJv8j1FP17Yfjc35Bq1ghN6xlzUVatChU4FLQB95S6GP3hLHSyq/wW0MChO+bO9IeuIhnbgg9DTJOkVCG4de9VXiE44z2PJyxC+ugzfR6GNNfHtbBtiLvLmlykFoc6UUHLsCHyMlr2HocDB3dhXGcHLlrKd/3MUX4bMfFXAD1neHV2EYKVvNmpF1y4dn32RBRuiWi8k3zuFC5QhWDPvnjzWY2Cfkv06U0VgmfxxxlZISighH2bwfh60wHE7F0Ln07OUBYXC68xSNp9JKXnAPUc0cDOUghWYlynPhzqcePh5BtIpg/Si4SU20kqhaBLw2oUgjdVIYaopcTXxtu+n+D/AnxgZ0j/LuKaAru6vZLcTOTmcsMaayuYqRPImJijDn0htwB5BQw38GdISxMUgrbVKQSz+T1LvIZZHfYpyMtDYT5gZGIKQwMh+CRGxrA0NuVGcrlIz2f0hxKeQ4ncTEEhaFqFQtDssUIwS1YIihGlQgFlNTcnhK76JAqUV4hn1We1CkEuTq/jskJQpJiZW8CYG8mUcxWsNq+LC5FDLwkGFqhjzuxTqM+gDQtbWSEoaQy4xDc14y7p2dkoUHdN5xI/q6gIMDXlhgV02lYc2FjLCkFJo21bF07WRkBGJrLynp+vVHAJkJ1JoFPXHnZ24jEuPFYIplShEExLo2owoFmjBvyeJeTEfxlMmsDNxQnIuYTTSU8bxSjJV88iKZNLAGc3NHl+tpNZHFu25hWCSfEJL1QIur0lKwRFiil8RvhAF7kI+m0Lnu7/srFl02ZkcRf73oP6wUqIigGqEOzdwQKP4kMRFPX04sKHxzZha0wWDNv1g+eb6qc7NRk58V+Slv0mIbCdNZJ2LYDvtO9w8nIy7l5KwHcf+mPB9suo22UCpg9qLZwtDrTMnHmFoGHFLcybGICf9sQj5X4yju35EaPHz0cyLDHz02loKisEqyKdzO5qTO+DyPxdSUKMPdIv7yGDOzry5YChFbE0VC2+q+c2iOy9liucpXn8M4VgNtm02I/Y6KjKamNrpSq/jg0ZvWQbUS350nz+JaGUIboOn4px46agc1N2B8G2Ld/BzkMx2PbjAgQO6QufIQFYsGoH4g6HYmALkf7Iha4lAhZsRlxUCOZNH4veXn3x7vR5CItJQPC8kcxNY/4Fn/5qqNkeX+bfRFYIygpBGRkeOfFlJEm1iS8rBNlHVgj+DYWgr6+vaBSCj2VSdJOaQtDf3x+TJ0+WtELw888/l55CkBaTKgSpRYu2fqoQpA1ACtBy0/JTdyhtBFKEKgTr1KmD8PDw6hWCgYGB6Ny5M68QFAOPFYKUCrW/Pi1OqELwm2++Qf/+/XmFoBShCsGQkBA+8WkjeOF0pqwQFAeyQlBWCEoSWSGIf1chGB8RhZvp7CsEH6PMvY+4o5G4ky2dG2XKndNHEX/+FtMqldeW+IdWTkR3bw9siGdYIfgUpdj6hT+6e/ZGCHVwSITC67sxrKcnfBdsAqMONZ7XkPgECZs+wZTPd3FHLCsEn6QMB1d/gBk/RAN6djDWlcbsUHHyUUx+bxpOc+3c2tKEYW9GbSd+2SPsXDoeQ95bjjv8g0si+AIl/w42zPPFqOm/IoNODOmLoSFXz/XoYIzoPwybY1UP4ugw3tZrLfHTL+xBoE8vjJi3Dg8tmqCZA13Hx/IUohJ3ErjK93bHu0tDUWbXAo2oSrCCPm4tYopS8Ms8P7j38cO+i6Vo4dwI9OFKBePFrrXEpwrBTUev4I2+E3Ho9114r1M9LsqoQpCnBPt+XYadCXfRceinOHg4BCPa6HFFEvf3AYqrhzBnaTBSzdpg0ZYD2LBwFL8UuUxOfHUoUbfdUHwbdBDRu9bA27U52wpBClGgaY8ArNgag8Pbl8G9rRPKSkqFF8VLhYkT3v9yNeISjmKh79uw1VVw3Rf71FLia6Pn6I/xsX9f2IpAIcijZQafdz/BR6N6woIO60uKuauX+G9qDZy98fncqejazJr/u5Qb2omh1LV7cysjo6HIiS8jSeTEl5EkcuLLSBI58WUkiZz4MpJETnwZSSInvowkeU2JT1CUl8Xti1BUJpK160SJwlxaliyUlLO7EONVUZQW8j/7k51Pv8Bjl9eU+EboNmI6JkyYhq4MKwSfQtcEXv6TuDLNQHtH8Tjxq8O2lQemTZiACQM7gf9SnlX4BxDVICsExYOsEJQVgjIyPHLiy0iSFyY+fTJfVgiyj76+vuTrkmoUn6RKoVRubi4vIKLquUGDBglRdnkskrK1teX1gbR8UtEIUjkYVUFOnToVPj4+QlRaHDt2DEuWLEF8fPyLFYKpqanw9vZGUVER32NUcRozKJVKXqW3d+9epKSkYNasWUhPT/+rQYgVWm8WFha8OY56ZWgjkBq0jmkeGxsb49y5cy9WCFL50MmTJ/lekZ4ohsSnDbhNmza8Ui8pKYl3gkoh8ekQh5adJr8YPKivCq3j0tJS/rPo2bMn7xCtMvFlZMSMPKsjI0nkxJeRJHLiy0gQ4P8BjIYNqFpiCqMAAAAASUVORK5CYII=" width="107" height="83"></p>
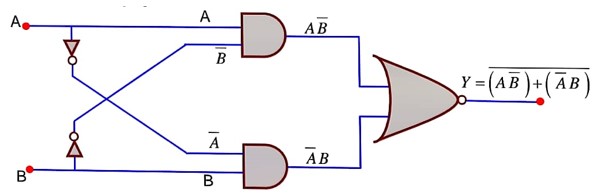
Option 2 - <p>Image 2</p>
<p><img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMAAAACTCAYAAADYxhZeAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFiUAABYlAUlSJPAAAB0eSURBVHhe7Z0HWBTX3sZfOrJUC0URW2zYSGJvECNYUFAkWBIbil2JV/OpV72JsSWa5JrcGBNj74qoFEUIaBRB7L2AYkVQemdpe745s0NAWRFNVjmz83ueYeb5zwB7ds572pzzjhbhgISEhqIt7CUkNBJJABIajSQACY1GEoCERiMJQEKjkQQgodFIApDQaKp8DlBaWors7GyUlJTwmxjQ1taGlpYWv4klTdVBR0eH3xQKhUaluyL03hsYGMDc3FyIvEIAiYmJGDlyJFJTU3kxsP7MjH5+ExMTGBoaQldXF0lJSbwQNAFTU1PIZDIUFRUhLS1NiGoOZQVegwYNEB4eDj09PWW8KgFkZGTAzc0NLi4u6NevH196sA4tBcsyvSaVhPn5+Vi6dCmGDBmCrl27Ml+YvS609I+JicHmzZsRHR2NWrVqKU9QAbyMnJwc4uTkRPz9/YWIBKvI5XLSo0cPEhQUJEQ0j6ioKOLg4EByc3OFCCFVdoK58/y+sLCQ30uwC60BaM1Hm0CaSkFBQaUm79sbBSrJxJkToTh69ChuJOYIQbbISriOUO7zHw0JQcgL29HQCJy/9RDsNxLLyX1yHUeCDnP37DgS817dZEqKu8B9F8EIO30dclZaWMqKQDXZ2dl8E2jXrl1C5M1JivieWHL/jv7LDyZvIoVCnCVifv2M//wv3cwakQHeX5KoR3LhN2oO6enppGfPnq/VnM2MO0i6mSrTNmCBPykW4qooSoomHs2M+Wvdlx4keQrhRA2C6/yS999/v/pNoH+OIoQEhSAVWqhlaICbwdsQ9ZS9slJHtxZfZZo2+RDDvIbDy8uL34Z7eWJwf2fYy54hZNMSjJy4EHHVKDFrOmbNh2DtT59DxrUaQtYtwo4zKcKZFynCnlULcCA+F036fIE184bAiJXBNUEIKvmnaoCS1PPErakhMW/dn8ycOJDLGfpk+sbzwll2OLfBhy/hPvTdIkSeJzM+nHi0N+Wu0SGT158TojWDN6kBeIqekRWe9ny6bfvNIwkqqu7EyJ9IM32uprDoQHZdzhCiNY93VgPERwfh2D05Gn00BjNGOqOuVhEO7N2PJEZHIRXFRSgWjiti1vRjzBg/mKslSnE67BiyhDjT6FlixtIV6GqthYTQNVi+NUY4IZB/B0sXrkR8kQ7GLv4RIzuUP2RigbcggHyE7vVDLnTxkWMntOjugp6NDZF08iCOXc8QrmENwjeMVVG7vh2XUkAuz+caBuLApJU7Vi/2hjEKsenrxQh7VCCcAf5Yuwi/n0yCbb85WDbNUYiyg9oFUPokCvvDbgIW3eDarRFgaA8vtw+4HBKLLX4nhKvYQktLGzrC8Ys8uH6Zz/jNHD5EXWVIFPSc+CWmD2yGwoRwLFmxk09jyb1gLFy9DyWyDlj17XzYGiivZQm1C+DC4UOI4fpOrfoPQscGysfPPd2HoR63jz64G5ez+RBT0PK/Ug1QnI1ov2/x1fpQGNR3xLRxH3FdfhGh3xDzVnwJB2Puvm39AX5nb2Ljqq9wLkUfo5auxvAOFsKFbKFeAShSERISypUWRnAdOADmwn+zfd8FLm30kH87DP5hccogC3A5mjZvbu1cjDatWqFVxc3eAf1HzsflvPb4fvd+DGrG5RSRYdFhNJbP94C+/BbmjPoEi9dfQJM+s7B8uvPbaEurBbV+7ty4KARGxMPQrheGubUTolw+Mm8LLy9X6JJMBAQGIvtlDeoaCC3V5ZnPEBcbh9jYWH6Li+P2d+8jp5Q7WZyECL8NuJgk568XGwN9V2Bir4Z4Fn8TKXU7YtkP/0ZjfeEkg6hVABdD9+JiDlDvvVYgD67iypUrwnYVhvUaw5xrSF8LPoSoB+WdqhoNJ1Q6cNV6xBJcvXULtypsN65fQ0zITozuqIuDPy/AZz5fI76AIWVXF+OW8HBz4guCls6fwJXRpk8Z6hNAyWMc2HeMP3x87Ef06NABDg4OwtYB/aatQSotMTPOYGfwef46FqBZ2siqEdq1avlX86dly1awb9MWXfqPwobtv6OvXS3cOvwb9oQz1Lx7DXR1lEMAhvovGwpgB7UJIO1cMAIuJUPLojlGeE/BtKlTMHny5L+2adOmYXjfdlxJUoKwHbvxgKEHw4riwpcOceo36YG+HzbjjtJx70GSMigyyqbF0z3rc5/UJIASHAs+jAdcE6Cj5yxs2rgOa39Zh19//fWvbe3atdj405f4gOsrplwNwqGTycLvsk4RcuTK2bNlJaVEzUUtAiBZsTgSEsH1GGtjkOsACEsPKiFr2QuufbnSUp6AwIAQsDLpWtdQhpf1+x4d34Og0/HcN9sEDu1oTSBRk1GLAB6dO4LDl+So1awnBjhWkQm0LTF4kCuMuMMTB/1xPqnmPzulX9jTi+HYsGUrtm7Zgi1027oVWzZtwJolvnAf4YurmQq0Ge4D9871lb8kUWP55wVA8uG//hfQeYOtnb3wwSumhrw/YDAcuGsUD4Ow/uDZyg+YahAlhbl8m/fxn1vgM34cxo0fj/F0GzcO4yf4YPZXP+Fypim6DpuLLWvmoD6DT0arQ3FBDn+fMnIKavT9qg7/vABKM2He2h1Tp07F4kkuL50yUIZO/e5YuHQRd/0kNJPV7E6VjYMrZnDpmjrl+Q49v02Zhi/+swpBx0/jz/2r0dGS4cHxV9C4q/L+TnbvBkMhxizCrFCV/JMLYiTeLW88HVpEvMMFMRISNRNJABIaTbUEQE2kJNhGX1+fd0TQ5HtZZoZVkSqNsXJycjBo0CCMGDEC7u7uQpRtaCYos0fUJGMsei/HjBnDd9j79+8vRDWLqKgoLF++nN9TlzxKlQLgOgv8MB+d7FVcXPyXTxDLUGtE6g9JSwNqjagpUGtEChU+9XsVw718HWi6qRuclZUVAgMD+TzAx6sSAC01xo4dix49eqBXr15ClG2oNWIZ1O9UU6DGWCtWrOCtLjt37ixENQs6E3nPnj0IDg6unjUiHQblMj7Zv3+/EJFgFckakZDIyEjSvn371xsGpSWmJtvpiQXJGlFp8VmxBUB5K8OgSbHncDgwAAEBQYi8fE8U9oEPr0UjOICmKRgxNxKEqLhRZD/GqT+CuTQH4Ej4aSTlCidYRqgJVPK3nwQrUsj2ZRNIi9o6tJ+h3AzrE7cZK8nNjBronVcdCh+RtfNGEDtjIT10M21KRiz4hdzPE66pgfzdJ8GxxzeTwZ2alKeZ21p08yCbjscKV9R83vKT4CIEr5qF0Ys24lmd3li+bjf2bf4eQ9uXIvDnBfD2/VG5IowlSD52LJyM6d/uQUELd6zeuA+71i2HS8N07Fk5DRMXbUW+cKmYyLp2AOM+9UbQhUx88q9vsN9/D76cMhAJpw/Ae/QYHLjGsAWYIASV/J0aIPvGHtLWAES7qTM59jBfiHJk3iLTe9pwJUht8lVQnBBkg+TotaS+Fohx2xHkQnp5DVb0LIZ4djAj0G5AfoxMEqI1izeuAUpSyArP5tz9MiIT1p0UgpQSEvG/scSQy0LveX1D0qtyzq0hvMUaoBTH9u7G9ULA3ftzfGRXYUmMWSvMXTAZMqRj544QMLIcnqMYR7dvQyLRw8hZs/GBRbnrj55lF8z//DPoKZ5g3+4wlbaJrJJ5+zj2Bt+BUavB8B1TcShcB32mLMCwlga4e2gfTj3IE+JsoR4BlCYj5sIF7q9bw7Hnh0KwHNsOH6GbBXDvdASus/KqgKL7OBFzG9BviT6dWwrBcuw7OaG1DLhy9jjusqPqV/Lo6nlclwPNe/WDPV25VBHdlnBxtue+mys4eeGhEGQL9QggKxUPHz0BTOqgUX0rIViOrqkN7JrroDT1FuIesDEsR1Ke4E4K19a1sUXDemZCtJxalvVhYwPkPo7HY1Zdf1WQcD+Wq8+Bpi3tVK7taPxeK+5nKS7filcGGEMtAijJy0JGCtckNrZCbeUT+OcxNISZeW36zhpkZbNRBRRmpnGflfvoFhYwfrEkpMhMYWnCVQFZucjOFU8VkJKinC5iXUe106mpBTW5BFLTMvk9a6hFAPL8NGRmcCW9gRlkqjKLngHMjDllkAKkpbMxgpCbnY18TquGMhkMVS11NKwFMyMTTinZSM0WwwA5RYHMtFT+yNSYS5sKDIzN+JohPzkNLPYC1CIAhaKU27gDLQLVM43KgvSlzWyMhfIeOCrTUg5/mpSiRERzjBRCWshLpoyVxRXFJXxTiTXUIoBaRnW5Jg7XMqQvklDVHC4qRGYOV/Jr1UIdlW2kmoeJmRmMjIFi7rOr1Gx+LjLyaBVhBktTsRjjasO8jrKJU8TdS1UUZmfwT/ZlVnXAYqrVIgBdmRnMuSZjaW4i0lU1DYuKkJ3NnTCoBXMuY7GAgakZTLhWQF5GBnJU1fUF+cjIzweMjWFK+wIioY4ggKdpqt8PlpuTydd8tetaqCczqRm1fGYtUws0aMApICcDzzIqd3JJfibSnnBVg4ktGjZgw1dAu64N7GpzHZqUVKRnVXZ+Ls1OR3oqga61NSzrVV55xCr17ZS+TgkJqp37nj1VzoNq3rghv2cN9YhW3woOrdvyVuEXrtwRguWkP7yIc9z3Vs++O9ooC5iaj1FTdGltB2TdxPnYypPfHt66hLh0LiO07IymbFRq1cLWvgMac/vYqBg8VYYqkIKzp65y+4bo1L6RMsQYaqq1DNDHbQDqogj7t6/HnecKzAL4rd+IRO6on5crLJVBBpBhwPBB0Ec2tv2+7YXMkIqtW3YgA3pw8RgItl4TVzVWbRzh0tkcKTH7sTns+YddCcc3Y1dkBow6uuLjNnWEKGPwEyJewt+aDVr0hCwcqJw92OmTeST87G1y/8Zp8r+5bqQWF7NsP4ZcTGbsddm5cWRq53p8mnpPWEEiL98ldy6dICsmf8zHbHvPInfKp5nUKP7ObNBL2+YSrldDtBv1IN/tPU7uP7hLwveuJt0a6xPo1CX/2X9NuLJmo2oukPoEwJH3JJJMHtiGzxyAITGm75Klmb/DAOJ3JUW4ii0y7oSQkb2aKdOkIyNG2so0Neo5nByNr6G5n+NvTYcuzSZ7v5lAbAyVaTU2kSnTb2hDxq8+QCpMdazRqBLAK9cE0zWkkyZNwsiRI4Xoa1KYjNB9OxBw8gbkCm3YdvgYY0Z74j0Lhu05chJwaM82hJ65i0Lo4r3OgzBmlBtsa/A4YEZGBn8vZ8+eDQ8PDyH6etw7G4SdfiG4nyaHYZ0mGOQ1FgM7cf0iRoiIiMAXX3yByMjIv1wh1FoDSNQcJGtEyRpRQqISkgAkNJpqCUCyRmQfyRrxb1gjDh8+nO9AiYEyW0S6aZo14rhx4/gBjX79+glRzSI6Opo3B3tta8Tbt2/zfjJVXMoMkjWiZI34WtaI1FCV2iI6OjoKUXahSaXGSPTLoNAaoOxY7OTl5WHZsmW8yXHXrl2FqGZx+fJl7Nq1S7JG1EQka0TJGlGjkawR36E1YuKtswg6dBAHDwbg5MV4UVgjllGS/gDhh4NwN01zOtSUO1GHcex87EvfmM8K6hUAScG2Zd5w7NEVbkM94OExBI7de8F9+grczBCDDAqwfclncB7khoPXReSF8gpybvnhk48HYdzSXWB99bMaBVCIwG9mYuzizUiz+hgr1++D/9Y18PwACP5lIbxnrUEK04VmPgK+n4J//RwF6FtCpqcZnenc+KOYMG4GrhQCdS2MwXqq1SaA7JsH8e8le6HTzAUH/gjCfJ9P4DHGF36hxzGjd32c2bEca49WXizDBOlxWP/FCIyauw2ZtCLTeystyXfOzbDNGObqBb+zytVhOiLQvJruXCmO79mNG4VacPP2hZNthWWPJi0xZ77SGnHXjiMMWSNSFIg/tQVuHzth8ndB0LZpg2ZWulxHQEy9GhXkPsRPc4fBsb83wmK10KZNM9BRdDEkWz0C4K0RL3J/3QpOPTsKwXJs2wvWiNERuMaKNSJPAY5s/AFBl5PQa+R/EBrmB892nAAKxd0BLo0Nw5ffH0CadSes2B+CTYu9QO2eiiUBvARqjfhYaY1oZ1N50aOuqbVgjXgbdxixRuQhCrTsMwFrD8YgZNcSdG9rg0K5+IcVS0yaYM53G3AuJhwLhnWHhVYx18MTB2oRQLk1onXV1ojyfGQyYo3Io2UCl9G+mDakC9eE45DLQZjvBr4agxZ9sWjOBHxop7yZhaXiSbVaBCDPTxWsEU1fYY0oR3o6wy9XkGAetQiAUBtB2j4UkTWihDhRiwAMqTUi18kVkzWihDhRiwD0ZGawqMMJIPeJamvEQvasESXEiVoEALPaqG9LrREzVVsjFrBnjSghTtQjAD1LOLSi1oiJOH85TgiWk/bgAs5Sa8Q2PdCWFWtECVGiHgEI1oj1UAz/7esR99zj3gLsW78RdC1Wfy9X7hoJiXeHmgQANHQcjcmuTZF8Yj1GjZ6H8LO3cf/Gafw0ZzjmbDwHqw5j8S/PTsLVEhLvBrUJAHo2WPD7NkxxbYcL/qvg3MUB7d7vDt8fgmD+/kD8sv17OLBuI04UyM2kw7jpKCjWnDW2JYV5/OuQMnIK/hrQZhX1CYDDyKYH1vlHIHTHfzF90miMGDsJX/5vL04dC4RHO0bdhCuia4wBE2Zh5sx56GynLwTFj1W7fpgzcyame/QA80MYwtJIlUjWiOJBskaUrBElJCohCUBCo6mWACRrRPaRrBHx5taIXl5ekjUi49B7SV3+fHx8NNoaceXKlW9mjUg9VcSAZI2ohawszZyCTt3grK2tX98asXfv3nBychKFn2RFY6RSEb3R/VVQY6yvv/4aQ4YMQbdu3URxL18HKvxLly5h586dkjWiJiJZI0rWiBqNZI34Dq0R/yIvCeGHgnHrKX2Qzjb3r0TikL8//P0PIerqIyEqbkozH+LE0QAuzf4IDD2FhBz2m1FvUQAEgd/5wHnoYOyIoa/JZpTCR/hprhd6de+NoZ6e8PQcip7csde8n3GPfV2/lNsRG+H2MdcXHDCES7Mn3Pv3glPfodgQcVu4gk3ekgCKceK3mZi2/DB3XBvG+s9XQ8xA8rB1vg98v/dDadthWLP1APb9/i0GvpcLv1UzMWHBJn6SmNjIuOyHsZ9NxJFr+Rg17zscCtiPpTPdkXw2AD5jRsPviqplf4wg9AVU8o/MBcp9RLYtGkXq0CqA3+qRFYfjhZNs8SzqZ2LDpcGk/afkUqYQ5ChJOUu83jcn0LIh/z2RKERrFm88F6g4mSz3oC8GlxGf304JQUopOb52PP/W/6aeK0lasRCuwbz1uUBPL+7DJ869MWbZLmRbt0LrhvRN0qw+fCpCyLZtSIIeRs3yhUOFpcw6dTthnu9o6JMk7NsdyrxleEUybx/H3iPxkLV2w6zRPYQoRRtOk+bDs7Uh7gXuQ+R9Nn2i1SqAP3f/gP2nH+DDIb74I/QAxna05qKFbM4hL3qAk2diAYNW+KhTCyFYjn2n3mgtA66e+xPx+UJQBDy8eh435EDzXi5oLQyd/4VuCzj3tee+myuIvPBQCLKFGgWggG2XT/Hz/hM45rcGju0bobiAXQ99kpyAu6lZgHUD2Nat7GRhWK8+rLn2Ud7je3icVCxE2SfhQRzo48KmLRpCVc+tUbOW3E8Frty+pwwwhhoFoI2enjMxfVhvmPLzr+jqIXYN9eRZ6aAzCAxrW8BYOY3keWSmsDThmnjZucjO44pMkZCSrByxs6pbl9+/iKmFclV3ahqbHeG3NArEPnnZ2cjjmrmGRjIYqlr8ZVgLZkacAOTZSOFEIA4UyEpP5Y9MZSb8/kUMjM34miE/OY3JETBJANVEoVCgyukz3Enl+VJRzTFSlAoe6C9JPBHiipISvqnEGpIAqomJmTlkXAFfXFgIlbOoC/KQkZ/N1QTmsDRTXVqyhzbM6yrt7QuLVY9tybMz+Iwvs6oDOsbHGpIAqomBqRmMuXydl5GBHFWjPAX5yMjjOvnGxjAzVmWJzSZ16ijb+E9Tla9FepG8HGXbv3YdCyYzkySAaqJd1waNanMZOzUV6VmVR7NKs9ORnkqga20NS9btXipQ364Zv3+ckMLvX+TZ08f8vkWThvyeNSQBVBejJujSphGQdQNnbz8RguU8uHkRsRlcRmjdBU1F5Pfb0L4DmnD7uKho3s3veZIRE3mV29uhc3vuu2EQSQDVRoYBwwfBADnYvn4Lnp/Ol4wtm7cjE/ro5zEAYvK7tmzjiH5dLJAS449NRx8IUSWPIzZh96lMyDoNQh97Nn2eJAG8Bi36T8LEbta4d3g5vMZ+jT8vxiH2wjF8PcELyw7egV2f6Zjh1ka4Whxoyd7D1FmTYKx4hMU+I/DNrnDE34tD6M6V8PRejERdS/zfv2egsRGjz3iUU4JU888aYyWT+d1q0TEzsvBgnBBjj8z4MPKZU3M+HYAhMeD3IE0dPyVh9/OEq2oef8sYqzSH7F89iTSopUyrkZGhMv1GtmTiDwGkQLispvOOjbGM4DTmC/j6zoVji9pCjD3Mmjpje9CfCNz0LWZMHoOxk6fi2w3BiDyyA86NxTP68xzaxhg29zecOnkYK+bPxKefjsHM+Stw9ORp/D7bjW17REEIKpGsEcWDZI0oWSNKSFRCEoCERlMtAaiylJNgC2oERV0hNPlevrE1Il0EPXjwYCHKNtQascwesbhYPPP2XwV1+ZswYQImTpwIZ2dnIapZxMTE4Jtvvnk9a0Rvb2/cvHlTFNaINKnUIpCWhtQkllojUiFoAjTdZWnVVGtEIyOjN7NGdHR05K0RxUBZ6U/RJGvEvLw8LFmyBEOHDuWtETURao24fft2HD58WLJG1DQka0TJGlGjkawRa4A1IslLRNiBINxMEsuSQaAk7R5CAw/hTqrmvGuAEnsyAH+cucW8BcxbFIACAasmot8wN+w8IxZf/jxs+fJT9HcfikM32HW8eF2yru+GZ98h8F6+BzlCjFXekgCK8eevMzB9ZQh3zLA14nPk4cDqKZj7SwygbwmZnmaMJmXfOQzv8b64XgzUq2PM/JNU9X/+3EfYumgMhk1dh0R+2J39zE/SbmPdbC98+n87kEXH0PRYzwbV41rIBngMHI4D55Wrw8RQjKn1ziVd2IthfXtjHFdV5trYw96OLhZnua2swJ0TG+H6kSOmrTkCfdv2aG6txyVJcE4QKzn38cPn7nAa6IOIu3po37456Ci6GJKtVgGc2PNfHDjzEJ08ZiM8zB9jP7TiooxaI/IUIGTzGoRcS4bT6CUIC9uHYW25crBQ3B3g0thwfP1jILJsu2LVwaPYuPAT0InfxZIAqkIBu66j8cuBk4jY9wN6tbVDEcPWiDyEwN5lCn4LPIcj2/6DLq2tIJeLf1ix1KwZ5v+4BedP/4EvhnSBGYq4YkwcqFEA2ug+bDqmDu0FE76xyLY1Io+WMfqOmo5JgzuCf44ol7Ofpmqg37wP5s8aCwdbpfNPYal4Uq0ZvTcJiZcgCUBCo5EEIKHRSAKQ0GgkAUhoNJIAJDQaSQASGo0kAAmN5i0KQIH8rDRun4/8IpEsRSQK5GbStKSjoJjdCR6vS0lhHv86pIycfIantSh5iwKQoc/4BZgzZz4+asmuNeJz6Jlg8JS5XJoWoVsjVS8OEyfWHQZiwZw5+NzLUflEnGWEpZEqkawRxYNkjShZI0pIVEISgIRGU6UAqIsA3SRrRPaRrBEBff3K/bQqjbEyMzPh6uqK4cOH8xaJZYZSLEPT0KBBA94UKzk5WWPMsajJGXX58/HxgYuLixDVHGg2j46OxurVq/l9tawRExMTMWDAAP7Le9FPhUXoy65NTEwQHByMhIQEzJ49GykpKaIQdlXQW2xmZsa74tFjTbVGlMvlvEXkxYsXq2eNSM1jr127xmccWn1UcSkT0M9PmwAtWrTgTZIePnyIEpVvvRYftACjfqi0xtOUNFeEFnLUFIzm5Y4dO/KFAR+vSgASEuIG+H8uJoYBhgvtqAAAAABJRU5ErkJggg==" width="110" height="84"></p>
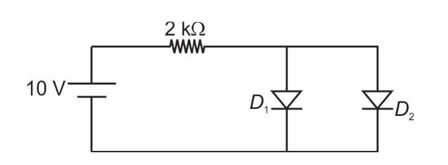
Option 3 - <p>Image 3</p>
<p><img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAL0AAACOCAYAAABkOQkzAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFiUAABYlAUlSJPAAAB6JSURBVHhe7Z0HXBTH+/8/VOlwdFTEAqjY0IgFO8bee4kktpjEGLGmqbHGGGNsMSZ+LbHEAnbs4teCivliiwWMxqigRqWX445685vZW5TDw+Qfj3+YvX2/XpvdfXbPMDufnX2mPWNCKJCRMSJMxb2MjNEgi17G6JBFL2N06Pj0iYmJiImJQW5urmjhHxsbG2GvUqmEvbFgYmICd3d3ZGVlQa1Wi1bjw8rKCk2aNIG/v79oKSX68PBwjBw5Eg0bNoSZmRl4r+Oyv9/Z2VnYp6enC0IwFlhaCwsLhb0U8vL/FZZulubLly9j6dKlmDBhgnillOgPHjyIr776CocPH4atra1o5ZfSGW1Moi8oKECfPn3w9ttvY+jQoaLVuGD536pVK4SFheGtt94SrRQm+mIiIyNJcHAwoe6NaJHhFY1GQzp06EC2bt0qWoyTZs2akS1btohnWl6qyFKb8FmU4ZviPKTiF/bGCtNzacqt9Sbu4PcIpZ/VoW/PxtXUAtHKFyTlGua+Hyq4B4MHD9bdhgzBuMlzsOvUdUin2q/CkR9mYOCgwXhnxvd4nCeayyLtJha+NxQDB4Ri3en7opEDhPJehLk3LVu2JEqlUrT8QwoekWmdPdkrJmwfbLoqXuALzf1I0shSm4YyNxNb0nn0t+RPlfijCkJ+fr7g3pT+tL+aQvL7iSWkqpA2S/LBmguiXR95ZPunXYRnYOk7iFx4rBbtFYugoKC/dm8MQWZcNI7/8hQu/o1Rg9aHI3/aiWTxGleYWsDWjj4ihyZYtHkvDhw48Hzbv3cXNqyYiaYeeTi+4VNMXH4UReLP+MUMvh0nYc38gfQ4H+u+/BxRD/R/x578sgFzlh8DbAPw3eaVaFHZSrzCAaL4BQxV0h9Z2FsoAcYt2UQmhXgQVKpJNlxKF6/ygybhCGnpREs9z77kahklefze2cSFlXY1epHYCpTEf1bSi2TfIePbugl5GDTye5KpEe3F5N4nk9pXoddNyKC5B0iBaK6I/P8p6fN/x67tUfSgNnoO7oNuHVsDefcQvjcK3FaPNQXIztRfL6nbsgdaVaHJfhqHm/ck0gFm54cvFi6EvwNwcescLD/wu3hBy39XfY7Vpx/Dq0MYFn3cE+ainRcMLvqk8/uw/4Yadq26IsjbEa26dYaPGRAVsRM30vh3AF6GtXbRnaUDnB0raU0SwKPVKCye3AsWBclY9ukcXMrQtgKp4vfg40Xbke9QD4u+mYGaHHk1xRhY9Coc3BWJFHrUvVcXuNO9baOu6NPUCZrfD2DnWY5q+CWhvr2Dk4V4okts1A6cfgZUadEbzdnbLRnM0GfqIoQGuSHj1nYsWn2S2vLw44KZuJJijkEzl+CtN1y1t3KGQUWvSbqGfYfPU6XXRa8urbT/uGk19BzQkR7kYtemnUhnniJHmJjSVKgf4sDWCOzZs6fEFoEVM9/F0PEr4BDQGd8tmgBP3r7zf4V9AOYs+Qw1LQh2r/kKixZ+hiXbb8E7ZCIWT+hKXwtOEX17gdetyMbvmUns6T/p1W4KeVgoGilpv24j9a2pH+DUiETEV7C2vVfAKrJtPK2ECt2rtgGztpE88TcVhdeqyOqgJj9P7/wivR5vkJ+vponXKj7lXJHNwdHwHcim1Zreo8aiaoliQNGoH4Z2rwNk3MSefafAUx+hhjnslSqj5/DRGDt2rLi9i7GjRmLIgO6oX9URu78ai7Yj5uNeNtOF1LDCsGlfoK8v+4yZYeD4uRgeqNBe4hSDib4o4RTCo+7So0Jc+OlTDBo06MU2OBT7r6ayu3Bo/z7cVQo/4QJB9E7NMG/teqxdu1bc/oO1G37Cjl2HEHVoI7rWtcT/ts7GzO+PIl/8nZQwVVSHb007emQP//p+4H3YnsFEH3twL35Noz6wpQ3uxh6lPu9u7N6t3fbs3ou4ZDVYVTD7f5HYfT5B+yNeIAVQZulvsvRs2BezPxhEy0OCo1FH8EQ6YxJeUFiAgiKtd1OQz+eQkpIYRvT5idi17xit29tg2OdrcfbCRWEcc8ktJvokPunvR29+hojtB6kzJB28vL3BBmLn5OYin9vOCOPBIKLPiD+P4zGPYebRGKFjhqNJo4YIDGyMxo21W2BgIzQKDMKoUcPhSO+/cXQbTj/gqc3eFOYW+pssGVcvXUIG3Xu5usFOOk31ksUgoj93eDtuqoA67foiuKpo1EP14N7oGmCNomdXsO/gOdHKAdS9ycnWTrt7samQo0zFKerLf7L6IK2t2KFvr97wLPvdkKkgvL7olbew8+fD9MAcPQb1goPWqhdT53ro3aMtPcpF+LYduJtTwVs7iAaE1dqSo/B2+8Zo0KDB861hg/rwr+WLkBHzcCdZg9Yj5mDa2825r+Tph6CI+vVAAYo0/LdQvbbon1w6inOPrWDv1xf92zKf/VVUQrd+/VDPwx5Ft8/jzI0k0V5BMbOEo7Mr7O2skPrnQyQkJDzfHiQ8QkauOYK6jsDXGw4gYs1UVLUUfyc5zGDjoIC9vQI2lvz3OuvMkWVDZtkc2aioqL89RzY/JwNpynyYWtnD3dFatL6KQqSnpqGgoBCVHNzgaFOB/YGifKSnZ6KgjNLN1Mwcto7OsK6APbFsjmyXLl0wevRojBgxQrT+Q0gRlJnpUOWDit8Jdlb8dD03a9YMEydO1HkGr13SW9o6wdPD/W8KnmEOhQu937NyxRY8g5b0Clo5ZaE09G2uLhVT8AbHxAx2Tq40za5cCb4sDFKRlZHhCVn0MkaHjuiZe89iw0gh5o2xY2FhIeSltfXfdTuliamp6UsREXQqssePH8eUKVMQEBAAc3P+fTeWNIVCIewzMjKMKtgTS/O9e/fg5OQEFxcX0WpcsGcQHR2NlStXYsCAAaK1lOhPnz6NuXPnCr2oLBQc77Ck2dnZCfucnByjEj3j5s2b8PDwECrdJbLZaGBpZqKfNWsWevXqJVop9MJz9u/fL4ynl5EGbDx9RESEeGacsAhnmzdvFs+06Pj0xSUhKxVl+Ia10zPy8v4qYpO0oRp/6QtfLq03hfm5wouTo5bWONs8Nt6GpkudZ0xDKYugYnlJt3yJzOs3rOhznmLPsk/QPtAXHtSP9PIJwKAP5+Hs72yqOL9kPojFV2FDEFDDi/rHHvANbIePl+xAYqa040Tej9mJ8QPaw8eL1gs8vNCkw0Asi4gB9xPEtF6OlteaI1uYRL4b3Zo9DmLr3ZiMePdd0r2Fr3BuVbMb2R/PX7AnRs6Ds2RYPSchHf4te5BxY4eTQG8b4bzekPnkQQWd8vu6c2T/OLGS1Ldl82LtSOveI8iYYd2IVyV2bkuGfHWwws0JLgt9c2QNJvpLP4URayqEKm9OJpcfaX9fqEohu+aPIJbUXqvXXPI4XzBzRAZZPrwOzWhTMmB2BElVa2e7K/+8SqZ28ROE/87Ks6RIsFYsXkf0BUmXyKA65gRm1cmCvb+SXCGBBSQhdhfpVNmKwKo6+eHsU+Heik75iT7nLnmvpSOBZVWy+myyaCzmCZncxpkKxJP8+EuSaOODzGsbSU0z+qWqH0pu5YhGkeybEaSeHYil/zBy458FjyhXXkf0sRs/IOb0hQ4cs4aULqeubgwjNvRa45HfkWzRVpEpt2gImXcvIuZSJhzqvIkOQaUDAHmiT7/OdP8Uh05f1Zo44drJKNyjlbc2PbrDT7t01XPs6gSjewtP5N89i+hrbNK7VFAj5sgxFKIS+vTtIMxrLklgSDc0cDPBrxdO4U4q+9jxh0FE//TBHSQUAFVrN4K3nulyVes2BJtLH3/xBvgJhJCHO/EP6N4SAXVqvRzYyMwVAbXrAJonuHGTRYGQCEWJiI9LosqojYCabqKxBFVqItDLEeTuHdx+xCZJ8odBRJ/29Cmy6N7R0w36QhtaOzuDdYTnPHqKNK2JAzLxOImV4HZwdnbSmnSwhLMrsxchTbhPImSkIDFdBdi7wcVGT26a2sPNxZ4mOxVJ2dmikS8MInplurZJ0p6KQN/gBWsbJyhMAJUyGdm89JUU5iA1O50e2MPZgWbyS5jAyZlNc6c6SU+TTrybzHQkqTWAqyNcrPUVYfZwcWe+XhrSU/iM0mwQ0RfkaTuhTMpw8Vh/GPsf5RdkQ82N6AuQW8D+WPrXlzFuxdRE+/jUKhW/YchLk58LldgJRet82oNSaNOdB6WSz95eg4ieTSFjFJWxqFd+nhpsDriNjSsceBnpamEDJxs2zb0ImjIyX5mjLekcFU602icR7GgJz+b6FtF0ay2lyEW28Ll2oO5dqdo9JxhE9PbOrsI/lEl9W30lnlqVKcSFsXFygz0vITLMbOEivMxZSM7I1Np0KEJmGqvJMNEr+I3gWxonJ7izOZBJ1M1R6VtpPAdpKWxslgIKhRGL3qVyFbB6fsaTJL2Ry9QpaUIF1rGmt3AfHzigWhXW/KpEWqq+VopcpKWxVFnDs4qn1iQF7DxRw4PWYdTPkJajR/T5WUjKohVYaw9UoS8IjxhE9J7V66ImrdM9jI/FfT2q/+N6LNiYv8DG9ThaqsUMAY1qU4++CFdu3BL+fh3ynuF63G+AZRU0CKguGqVAVTRo6k0d+t9xJf6paHtB0f3buPpYBcvafvDz4nOGnUFEb+XzBjq2qYbcuyew+zAVQkmyrmHTjpOAeR30CWkoGvmgTkgvBFG3PnZPOM4/0nXcHp6NxP7YTDg17ob29fS17vCKCYK796ffOQ32bQl/aVXIozsjcIt6da1DeqDWqyJ7VWS0HbNaXmfszd2D8wl1XQi82pEfDl4mKdnZ5OGtC2TG4OasFkhajl9LMsR7+SGPbJ0ULPz9tbuEkTNxD0h2diq5fnIz6eZrR2CiIJ/vihPvrVi81oCzrLtkQrAjTbc56Tv5R3LrUQrJSkkkR9fNIn5mNI89m5N98TwMQijnAWf0SZF980cTDyZ8mJFa9esTTxt2TAXTeQq5nlpiaRKOyEu+TT7v3VRIB6zdSP36voTWxem5Ixkwe3eFHX/yuqMsn10/QPo0cBfSbeNViwTU0h7DqR6ZuydevKviU84rkdijz8y1OH1qB8JCe6KyoyP8Ww/Agv/sw+l9S9DAmc/2DUtXf3y56wiObFqMwR3qw9HRE28OHY+tx6OxfU5/YXiFFHFv0BMRJ05i3cJJaOtfGYrKdTH8o/k4ee6/+KJfXfEuThHFL/B6Jb1MReJ1S3qpUM4lvYwMH8iilzE6XhI9mzkuhUBPxg6LcMaQQvyi10FfrKOXQnXPnz8f1LeHjQ2fXcwlYQkuTjRLZomkSp7CwkL069dPCFE9ZMgQ0WpcsLxv27Ytpk6dqhOqW0f0p06dwuTJk4WYKfreEN5gSXNzc4NGo0Fqaqok0vR3YWl1cHCASqV6HgPH2GD5n5WVhdWrV+tEONMR/YkTJ4RFGVg8y0qV+B83yJJW/JmXyov8dykqKsKKFSvQqlUrtGjRwqi+csWwNM+bN08oyPv37y9aKUz0xbCwfvQBiWcyvNO+fXsSHh4unhknTZs2JZs2bRLPtOhUZFlJyDY5rB//FH/Z8vOluIb534c9AxauuySGb7LUZOH6L2dw9OhRHDt5Dg9SpLaEdgHiL57E+fgn4rmRkJeM6OhTuPUnP1P7y8Kgos+IP4GPenVEUMv26NatG7p2bIPg9l3w5dZzkplO9+e5dejYtiPeWX5ctBgHJ7+bhHbtQrDi+D3Rwi8GE31h8iVMfns4Vh2+hhbDp2Hzzp1YNmMMzP+Ixsx3RuCrA7fEO/kl+fJOjBzzGZ7Sj5ebg7EsDU4Qs2kWxs7cRo+d4WDFf7u/gUSfj8gVX2Dj5WS0C1uPI1u/QejAgZi0YB2iI5ehhlkCvp6+ANczeA17m4eYPd+gS68RiLqjnTpoFO1AeY+xY9FY9Bm1APeFOfLS6LQ0iOg1KdexJfwYoGiMKROGomS3VvVO4xE2wB85t/dg7/kE0coP6pSbmBvaFSEDPsbVJ7ZoVL+mYJd6A+CTK5EY3rkdhn22AUq3mqjjo6CJloaTahDRJ9+9iht3NfAI6IDGtUrP/LZE606d6D4XUdGXtSaOSLy4G9/8fBq2Dbpj84kTWDmho2Ankm73Joje9j22R/+BwN4TcfzYAYwNqUbt0mgJMojonyXewyO696zpB3c9332X6jWoNwg8vPYbeIsFZu3VFIuW78Cls/sQ2rEJrAul1hqlj0J4txqKDdtO4szuFWgTWB2FElpgwyCiz0pOpl4vC+vn8lLAT4a1g0II66dOSRXC//FEtcAemBA2BDUcxZ5daa/DIGKB4H6jMGpYBzgIbrwKGgnVYgwiemWmNkKltZ2t3n+wUiU72NFnpsp5hky530vmX8YgoqcObvGBuNeFEI1whdDywgiHgMhUMAwiejsnbUz6PHWeXtnnqrOQSS/Y2nnAUV6MXOZfxiCit3d1AQt/mPks9eWgSJRcZTZY67aNqxscjWego0wFxSCid69aHZXpPiUxASy4dWmynvwp2N1q1xQqtDIy/yaGEX3NhqjjDTyOP4tbz0TjcwiunDtF/2uKNi0aiTYZmX8Pg4jezKsR+ndvBs2TaKxcHanj12ddj8CqHVdh4t4R/dv7i1YZmX8Pg4ieVlExZOI0tHQ1xd55IzFk2nKcio3F/g2L0K33WFzJcMK782ahhSfz/GVk/l0MJHrAIWAQft6+Fj0bWGPnt5MR0rw5+o75DBcyXDB63hosea8NRxGLy6ZArV1nKSOHz1U4/hkaqISliJTIyeN/rXyDiZ5R883R2HfmHCK3rsWypUux/PsNOHPuHNbPGgypxPWt3fVDrFq1CgtCW4kWY8ABfScupeleg7eCq4o2jtHOGtQih/WTDnJYPy1yWD8ZGYosehmjQ0f0tOQXZo7b2spjBXiHxfthkQCsrXlZzrF8YGENma5LohPs6dChQ5gxYwa++OILWFnpWziXP1imsyTm5hrDOPgXsGBPLHBXu3bt0KZNG9FqfISFhQkBn4YNGyZaSok+Ojoa06dPh1qtFkoJ3mFJc3FxEfZsJUAppOnvwtKqUCiEGEZ5ecbUvPqC4sJu+fLl6N69u2gtJfrDhw9j8eLF2L59uyQCuBozLIDr8OHDMXToUN2QdkZGz5498eGHHwrP4TlM9MUUh/VjzV0y/MPC+m3btk08M05YWL/NmzeLZ1p0KrLsk8g2Yw8FJwWKw/ox396YKdZ0Scq1yfLSrq8xadEWJOtbbZ0rCnHz9E7MnDIe48a9h+nzViLmtyTxmnGgeXQeM2Z8gp2x/IczLDfRp17dgfdHf4oVP+xDGs/1qMIsbJgyGK06DMaXy35A+I5NWDI7DO1adsC09TGSCVf4SgqTsezTiVi4cDGi4vh/2ctF9AmxOzBo0HhczqafF09nmHHbaEJw5seJmLRsL+yav4Xw/17EjRvXcGjDHASQeHw7KRRrz0k8kKs6AcsnvIXPt16hJ25wsuZ/2KBBRV+Y8wwHf/gE3bsMw6k/tHOoeG4k1KTE4MsvNyHbvhlWbVqHwSFNUc2nNrqPmo2ff/gMDsp7WLhgDZJ0+z4kQhESr+7HBwO6Y/KaKG2Yp1K+Ma8YTvSFiVg4rDN6jV+M+AJfjBw1FB42VDiF/AaK+S1qF04+Ber1H44utXU76xr0DkXvhjZ4dHYvzv4uvY6vaxGL0KZVX/x4JB7Nug5F7+Bq9MMnjfZ+g4lek3sfF2ISEND+Hew+fR7rPhkAYTBDEa/FoAZxV+JoeWeKlk0DdeJzCthWRbMmdQHVXVz89b5olApFuBl7AUqnOghbugfH96zBm3UcqV2OZakDsfDHnD0nceHkRvRv6g6z3BwUcP2MMvEgkU34tYWbpzbEiS628PTwpHsVHj5gQQ2lBEGLt2fjbHQMlk/uB0frIihVLM6F7N7oYFbJC83bNoGD+FwKNZw7uholkjMz6IED3JyctDYdTOHsxko/IDszk34XpIQ5ajUMQoCvQjyXVlu/QSuykiI/F1kqNjXQAhbm+hciqGSpXZghMz0dxjWcjW9k0ZeFmTkqWWgnspfu0SumeH1Wtvyoca/LzRey6MvCwg6uDuzznoMMpb7FxQjS07SrkihcXWAsi/FIAVn0ZWIPDxcm+iykZegLMJ6P7Az2MpgLopfhB1n0ZWIF/9redJ+He/cSdQJYCZBM/JHIVtpzhq+vj9YmwwWy6F9BgzZtwRolz0adxJNSDRiFidcQdSEBJt5N0SbQS7TK8IAs+lfgEtQf77R3QerZDfhipdgVz8h/glVz5uCXFKDTiLFoIns3XFF+oicEwlDuIo5bsM288OH8r9HMKQfrp3RDp6EfYsmSuRgQ0hqTN8bAre37+HpKH71LDkkNjUbITGheTLTjlvITvYkJzM1NYFJGGzcveLceg/AjuzCm1xuIDV+N6dPnYM8VNfqNm48DG5cg0NU4PpZmZuY0S81hJoFBZ+WWY2YB/XH65m3c3r8QPpzH9Kveoj/W7TmB3+7ewe3bt3H3tyvYtWYmmtcwllApCoxbeoSm/Qqm9/ATbfxSbqI3qeSAGr5+8KvmAQspFIbm9vCp5Qd/f3/UquZpZJUhMzh7+sDPzxeu9vxHnjauvJORociilzE6dERPaM1cDusnDYrD+hl7Xv5lWL9jx45h6tSpaN26tfDQpICjo6OQ6Kws3tYqfz1Ymi9evIjKlSujalUJxJT/h+zdu1eIcDZw4EDRUkr0Z86cEeJY+vj4CG8I72g0Gjg4OAgCyM7OFr5ixgJL85MnT2Bvby9sxgjL/5s3bwqxLHv06CFaKUz0xbBFGYKDg0lRUZFokeGZkJAQEh4eLp4ZJ82bN//rRRmozegi/EoRFsuS5aWxR6tjpX1p9H7v2cOS4Rs5D8umHJ3cXGyY3Al1e3+MBO2CfNIg9RKGd26EnvMOiAbpkhR3ArPG9YV/tSqoUrUa2vR9D5uj4l4MvOOUchK9BmfXz8Qny1nX/Z+QwCqMWnIf4ZtpYdgedR2JydpZU1LlSewW9AvphgVrI2HhXR9v1PXE1f3/wTudO2Lij2e5nipueNGTTESuCEP/cd8ihZ6aOljDVAKRI/JT4zB33DB8vDFGOLerJIVVcfWjyYjDjA/eR0ySM6atP41zJw5j/+FT+OX4WrRwSsaaT97HtivaCHY8YlDRP7x6DNOGdkWfSauQojHVRoHj3bXU5ODC3lXo+2ZHzNlyDibm0h9IfOPoeipqFeoO+wzzRreFwtoMJha2qN9pLL79ciwqZcVj9X92g9dg1IYTff51fN6vJ76N+AU+bUdi/fez4WNLNZPPt2/z6H9bMKT/RzjyayZ6fTAXKz/uK9ilMK5cP3k4d+gQ/a85+g7qitLLtAV37436zsDFc1H4PZ3PZ2Aw0RfmKWHl3QYTvtyM6CM/YXSn2iAsQgbn2lAqc1GvzUAs33sSkau/QNvqEu/o0TxE3PWngEltNPTzEI0lqOqLxlUcUXTnNn57xGcvt8FEb2rTGIsjD+K7z0NRzYa+BEo1LQ3FixxTPXgUIg6HI6xvS+FcmauNdSNZMpKQkKaklRZ3uNjqWWHS3AHuzvTFL0jG0yw+K/OGE72ZNRQK6S3OZmXrCHs7g1Z9KjaZ6UhSawA3J7ha61tW1R6uHmwQWzoyUvn06o0oN2X+FrlqKFng3TKnBZrATBjDpEZWFp8997LoZXSxtYeCNVBpNGVUx/KRk8O6p+zg5MznauSy6GV0cVLA3doMSE5HskpfSa5EanIO3Svg7MynOyuLXkYXB3f4uNGKak4K0tR6RF+YjdRsWtG19ICXo74Q5hUfWfQypfBG/caVAXIb12+zRSl0IQl38etjJcz9a8HXy0608oUseplSmCG4ey/YoBD7tu9H6UbJ05F7EJcBNG/XBX58FvSy6GVeJiDkHQwJrITfds3HpAUReJyuQoEqDbF7l2PKrE0oUNTH+DH9oK9BkwfKT/RFBVCySn5OriQ6qYopytf6uao86XZSmTjVxezv16KtD8HGWUPQrE0IOoe0RnD/yfg1zxuTl27AsMacFvOUchO9ib0ngls0RdOgOpDAervPcaxaF02bNkUTXz1d9BLCJzgUB06ewNdTRsBTk05Le6DD0DDsPnMK34wM4nvJNVICNke2ZcuWRKlUihYZXsnPzycdOnR4aX6osREUFPTXc2RlZKSOLHoZo+Ml0bOoWFKIeWPsFOehMcX60Ye+lSF1ngh1d1BUVCQsFclCJ/C+sfSwfTHF58awsTyUUl7+0409A5bvJdGJcLZjxw6EhoaiQYMGemMA8gZLdJ06dbBu3Trs27cP69evF2L65OXliXdIF1bCFWe4MX65WfpZ2q9cuYIVK1bgo48+Eq+UEv29e/dw6tQpIeinvs8Cb7CAR+7u7ggJCcGdO3cQFxf3vASQQvpeBUufQqGAWq2GSqWSfHr1waSdkZGBdu3aoW7duqK1lOhlZIwBufVGxsgA/g/TcXqHO58kEgAAAABJRU5ErkJggg==" width="114" height="86"></p>
Option 4 - <p>Image 4</p>
<p><img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALsAAACTCAYAAADWb2gxAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFiUAABYlAUlSJPAAAB7CSURBVHhe7Z0HWBTX+sZfeu9FREVBrFgSYwOxIFhQLNgVNCKxokZjYgmxBI3dJDf5W3LV2IgaBRRQsKGCvcQoMcZCUUBUlF6Wssv858wOKLokudnlXs7s/J5nMrvfDEnOnHfPfOfMOe9oMCwQEVEDNPm9iIjgEcUuojaIYhdRG0Sxi6gNothF1AZR7CJqQ/XQY15eHh4/fozy8nLugBDQ1dUFKV5FRQUfUR9MTExQWlqqlmWvgtR/o0aNYGNjw32vFntYWBgCAwNhZ2cHTU36G3xSLGtra1RWViInJwcaGhr8EeFDymplZYWioiJO8OoIqf+MjAxs2LABM2fO5GLVYo+OjsbKlSuxf/9+GBgYcAdpp0rgfBHVBqlUiqlTp2LkyJHw8fHho+oHKfsnn3yCiRMnygNE7ISoqCjGzc2NYS8UHxGhmT59+jAHDhzgv6knXbt2Zfbt28d/Y5ga+Qr7XW1ve0KC5OnkrkZaeHWG6PlNaqQxa9aswenTp2FkZMQd/Kdk3DyG/SfvoELHEROCxsLRSIs/QhEFydi3KwxpRVIFaZAGTGyd4N63Hz5wtuZj9Qci9gEDBmDKlCnw9/fno3+FBJci9uHM71kwbPYBpvl5w+zPum6lmQj79y7cy2HQYfBkDO/SmD9Qf2BbdsydO/f1NSBiJ5A0xtXVlWE7NXzkH1L5kgkZ2Zyog920mc8jH/EH6KIyNZJpr03KUPtmbNeSmfFVGFNSyf9RPaG8vJzx8PCocQv/a8qZ66HzGX2ubJZMSOQDPq6Ys/+aKL8OJm7M0T9y+Wj9okuXLrWnMapAknQVJy4kw9CuGWx0pDi86yiK+GNUoakLUzP2jmTUErOWreV69VXb2tUh+HT6KJi8fIhtwdOweM8N/o9oRgdd/FZiy8xe7OccbFq6HLfYVlsRhQ+PInjlAfYaNcTyvTsxrLU5f6Sew4teZS37hc2TGFYizJjPv2ECu5mxv/yOTPhDCX+UHiqfxDKuZmzLZefL3C7lg29xfssMxoC08O38md+L+WA94J+17HKkz64wvi76XKs9aHE4U8bHX5PNrB3bjjvec9p2poCP1kfqtmVnMhF5IAoyNIav/1h4e7iyzcAdHDoSz933qYOMXFaWoyBX8YOZ3sP90NMGKEq9ipuPJHyUbrTsumNNyGL2rgzEbFmCvVdf8kfkJO5fg/U/34Why2hsWjUFJnycBlQq9oJbx3Doch602/dH9zYN4THIC+TZVfThCCQVUSn3P0fbCIZ67F5DF3q62vKYAGg1YgFCArqyFfoQIYvWIpl/qF759AIWLvsGOVr2WLZhLbrYqDwLrlNU+H9bgTPhkUirBLyGDkATNmLZdTAGuRig5GYYjt7IlJ9GGxpaMDBkmzkFPL59CpczALO2HujiqPgcOjHGlOUbMdjREOkJW7Fx7y9c9MCmYJxMlqHn7FWY7e3ExWhCdWLPv4ewqDi2n9MUQ709wA026rXGMF939kMODoQeA203eu4JbEU+/ridiHv37r2xJSJ27zr4T/sKhdZtsXzFPDjp838kEHTte2L1uiBYs7W2+7sNOHjgO6z+/gJMXcbhmy8mQ7nB6f8RfO6udAf18amNjC37r7P44CPmwRv90WeXtjGOWmC07HowsU8q+Gj9h3RQezbQ4zpif7aNXhHO/0X9QZkOag0qXzEb/N7nymlkpMXAoCmz/lQqf7D+U0cd1ArERfyELPZG4T15Olq+0crZuY3DWC8HyJ7fxNFjV/koHTCVbE6mZYr2XVzRo0cPuLm5yffdu6J9W2dY6mvj2JbP4LciFLky/o+EhIYVgkK+RB97DRQXy+A5bSXm9GvGH6QP1Yj95VUcjLrDfcz65TBWrVzJTSoj26qvvsX9HJLUlOHo0UhkUDSDWEamx1r1wtbjF3Hx4kVcunRJvr9yDYm/J+L04fVw1kzF/i9nYsWuqxCi3g2adMIHLqbsJzN07dkNNGdrKhH77ycicDmTbQVRiTO712PpsmVYxm9Lv1jBdk5TufNenD+CYzezuM9UQW7k72CATj7zsXHeGGijCIfCw/BcOEsBXiOtgJRULflI+Vwb5cUuy0LYkRgUQwf92A5bGNt6R0SEIzxcvkVEHMGRiIMI6NWQzXaS8dOhM2zSQxMMKitrb7NbubiAPD/MKShAiRDF/iaUT5VWWuwlSdcQe/4hYO6CaQsWYeSwofD1HYERI+Sbr+9wDPcdiwUzxkCXPf9G5F5ceSH/W1rQ0Kj9MqU+eoQCdm9hYgJ9IY0+ChClxX7jTBh+yQUcXX3Qq0Xtsxtb9BoBTwctlD2+gqhTt/koBbBC19FTXK7kS3uxfNsRlLOJTD+P/mhIHjCJ1FuUE3tFBiIPHAXJ5PqP8oXtn6x80230AYZ6d2c/FeDnnw/jGQW5jIYWK/JXF/HxyIEYNGhQ9TZ40EB49OwCV88PkfCwCM17zcJn07xYyQsThpH3xyjPYpQTe9bVMOy/xN7EjXtgpFc7PlobRhjqOxhk9ndG7CHE3q4556LewVawTMrm6rJcXDt7ErGxsdVbTOxJnL94E2jaHQELv0bY/vXoYFH7XY1uGLaPSjoj5WxHlW61K7V4o+hFEhKTX0LD1B6d2zVlu6h/QXkeEn/7A8WllbBr+T4cbQz5A/WQsjz8fvcBCsr5oYi30NLRh03j5nC0I8Ny9Yt/tnijFirL8Ph+Ip7lA/YtXNDUuh7X2VvU/eINkf85KnuCSjl1vnhDRKS+IopdRG2oFjvbynPmSMouthb536Ojo8PVpbGxMR9RT7S1tTldV1HdQT1x4gQ+/fRTDB8+nLtYQsDU1JQrbGFhIR9RD0iZyaiRs7MzWrZsyUfVj507d2Ljxo0YM2YM971a7AkJCQgODoaZmZlg7O/Mzc25fX5+vnxuuppAyiqRSKClpVXtd6lukDKnpaVh9erVGDx4cHWQIzo6mnF3d2fKyt5dYitCH56enmrvCEZGF0NDQ/lvb4zGsJ8hk8m4TYRuSB0SQ1d1r0syS5Pouop38hVykUTopqoO36xoEZUOPZbj1+M7ETDMAx3at8d7bgPwxXcH8aSA7jnQlcVPEb55KQb26IT27Tug99AA7Ii6DokatQmFv+7HwIH9sOlECh+hExWJXYKokCnw8PkIu4/fga6pKYqT4vHVx+PRZ8hs3KB0VUNlbhI+H9Ufo2avQkJyEcxMtHHn+G5MZX/QI5eEIk8NBF/x4jY+m7MYJ0+eQepLKr3dqlGJ2JNivsW05T+hvN1IhF/+BfHnzuHKzRtYG9AHjxN+wOxlu5BH3R21DD9/FYh1J+6h+4drcf3GZZw7n4BbV49gVDtdxK6fgbVhv/PnCpPi1HgEjRuFHy6lAxq2MNShfLIb6aUS/vHcmLKnzKIB9gw0LJiQyBQ+yFN8j/Fvr89AswVz4Lc8PkgHkuRI5n1DMBpNfJjLL/kgz7OELUwTbTCmnWcyKfVw8ErpuTGSV0xc6ErG3cmQNFHyTcOG+ezAXf4EOlD53JjilOuIu5gJgxZeGNLXkY/yGLaB3xgvNh94hKhziXyQDn47E4VfSwDX4SPQ+S1Xartu3hja1QIFd04h/nfhPbBK2PEFPP2X4mKqPiYvCMH0wS1ZuZfxR+lFabE/f3wfqcVAkzad4ajg6bRTxy7civRb1+6wiQEtVOD+b0nsXhvvt2/97tRl3Qbo2K4te1o6fk0k5wkJKZ6zuXm33qOw88QF7Nq4CK2tyBWgv4OitNizM58im92b29spdIkytLbmFmwUpGagni/XeIN8pGe+YvfGsLS2kIdqoAdrGyt2X46sTMoW1P4lGvCctR6nYg5jSn/2B40CSMqFMV6vtNgLc4jUATNbS4XL0gyNLWDJ7iWFr1BEi62ArBivCnLZDyawNjeTx2qgCQtreTw/N49bligctGDVoCFM6Vmj8bdRWuxlJfKcVbOWqSeaGlrQZo+VluWgiBazx4oyFJexCTtb8bVdIG0t+U+7qCCfbd9FaEBpsesbyZelVXJm5u8irSgFeSWZvr4FjGhZfa+tDxN9kpSxeWotE8iqXrRmbGr618sRReoFSovdxFI+VFHwKleh/VtJST5yGTadMbWBKTViN4KVKbE+KsSrfOIK8zaVyM2Rx82tLESxU4LSYrews+Ny8oLnrxRaUpfl5iOP3Rs7NOI6qnRgCvsGpANahFz2//9dythcncTZjmoDW3lIpN6jtNjtmrZCMwMg4/6vSFcwtph+/w73I2jTsQ0rDVrQQWsXYrZfgd/vJ717x5Jm449HD9mrZ4s2reh1tVU3lBa7sWMn9OhihcKHZ3DmbV87WTrCw0+zH+zh4/GePEYJ7Tz6o5UucDk6Cn+8lcnk/xaPY1eyoNe6N/p0IPc1ERpQWuwwaIaAQD/ol2fii3mf4vTdF1xLKMl7it3B87Htaj5a+AbBpxM9SQzBqI0PZo1qCcm9g5j72fdIzSWjM5XITrmExfM+x0OJFvyCZqK1uGSXGpQXO8v74xZhXYAHCu+Eor9bdwwbOxYD3LsgYF04jNuMxOYNc2BH3RwiE3z45b8xoUNDnPv3XHRz88LYscPQvUsvbEtIQ+eAjVgZ6FbLGJSQYFBRRkaeSlAho/spqkrEDl17zP0hAid2rMKA1nq4HheHB4UWmPjpBpw7+SP6NafpBYKvMXPujR2nTuP74EA0LH+MuLhrkDr0wYqtkTj2/TzYq4WRqTZsmrSAk5ML7Mwof3EUPyFMhY5gMkYqlbJbPXvHuZJUykiZpIyMgmKp2hFMVl12uur0v+AIpsmtatfSEtYNXkOTlEmr1ifFQkazuux0F74OxC4iUj95R+zq5K8iVKrqUKzLmlSLnU1puI2Y6ojQTZXtG0k91B1yHaqodgSLi4vDvHnzYGFhIQhHMIKVlRVnK5GbS6brqhdkohqpR3VuvB4+fIgtW7Zwlo6EarGfPXsWq1atwpAhQwTh9UiKZWBgwO1JxavTLZ38wIl3J/F5JH6P6gip9/3792Px4sUYNmxYdZAjMjKS6d69O/9NhHb69OnDHDp0iP+mnpChxz179vDf3hh6JC0f2YqLi/mICK2Q18yQuiwro3+RtLK8mZKrPDnPfpaOlJQUpD55imJhrVfjyH3xBOmv6DYL+rtIi7LxJDUFKampeJ5DfyOoMrFLs+7j/xb4oYuLM5o3bw4nx5boN2oqDl+m2zLtTYofRMKzaxsMWRnFR4SKDDcj/oURXt3QzKk5mjs5oV1XLyz49gieyRdoUYlqxC5JRUjgCMz5ej9kLQYgmO3ozhjZGTcjd2DMkHHYdS2TP5FeKjKuYO7Uj/FrmgQ6Ans6/Da3Dy2H78h5iL4tw/jZwQhZPB0Oklv4ev4I+AfvAbVOOXzursTcGBlz7ttJDFv9TJsxq5knxXyYqWAubP+EMWfjdu7zmOQSeufKPPklghnRpZHcGYvdXBfUb99zZebGlKafZ/o1Zstp3IHZfjmDjzJMQcoFZlxbKwaa1syamFQ+Wr9R+dwYpuA+du4+DMaoBZYsmQOHagsGbbh/tBwfe9vj+cXdiLz2jI/Tg7TkKfaGTENvjxGIuPEUDbilenLFC5XrUTtwOgPo8dFifOTaiI8CJo7uWLlyBswqX2HPnkMUeneqII3JTbqJXxIlsGztCbd2b1uCmaL/kP7sPg+x8b/IQxSRdiUUc5Zvx2PNNvhiWzh+WDiEi7ONBLcXHkW4ejqB3RvBh3v1fk2c3TzRsaEm7l+/gAdZ9M1tV1rsz58kIY0tN3n7sb0ClyQ75zas5IFHt+5B0dLl+gxjYI8pM0MQdzkOK6ePQBMDIbfpLBVp+ON+NquKVnB2ULDcsIED2jVgE9PHyXiYSd9TaaXFnvciC2RQyqyhtcIF1QbmFpyrgORZFucyQBNOrv74ZstS9G3TkPteKqXf7/BPyctGRkEJYGEFawMFCzU0TGBjw969mRxkF9I3/Kq02IvyiCciYGxuqvBfZmBgCjO291pcnIUCWhzBeNRu1mB+Ll5K2LuXhQnM9RU1XUbs74B0ylixv6Rv3F1pscsqeAPHv8hjZVIJygX4kElQSCtQRm5ebFXW2i8h426oQGkpfZWptNiNzOS5XYVUpnCUoqy0CIXsAUNjW5gJ0CxTUJiaw4Y06BVSSBWKXYL8fHJ7Noe1LX2VqbTYja2sQGZN5794pdDNVlJcwHVMDS1sYCpOr67fmJvD1lAHeJGDrBJFOWcx8nKIpYgFzClsuZQWu00jB9ix+9ynzxQ+WSvOeslmeOzlcW5Kkf2dmmJoj+b2pkB5Jl4VKhC7JA+ZeQVsC9cQDpaKfOvrN0qLvUGztnC2AdLvXUaSguGWP25e4kyTunZur/x/TKSOaYiO3ZqzeXkKrt1O52OvKXt0F7cySmHk0gYt7A34KD0orT9dh04Y1Lc1Kh6fxZ6fr/FROUxmPLYfuMC2GB/At68LHxWpz7j5jAGxaj36406k1DCel+HwnlA8YrOYvgOGwZHC/pfyja2mJSYGBcFJuxRbPpmCpdtjkJSZiTsJRxAwLhCn0jUwaMFi9HESe6c00NR1AqYPboxnFzbDf+JSJCQmISPpNnaFTMX8r09Ar6U3PgkcwPXTqIObIcOinElSOXNpRzDTzlyLdOEZI0tLhr0Y7GddpveH65gnJfxplHN+3XCufK2m7+Ij9RNlTZIKn1xhZni15coKbSPGwkiT+2zi7Mlsi3/Kn1X/qSOTJB24Ba7C2ctnsSF4LkYMGgT/afOxKzoBJ3YvhAN96Z1CGncZiunTpyPAS9gpmbFDd2w9FofjezZhut8IDB4xCYvX/YirF45hei97/iwK4UWvQvs7kf81qra/o5X/gv2diEj9RBS7iNpQQ+xk4pO+PuW2xCKc7w+pSyH4/yjD22Zf1SZJ0dHRWLFiBXbt2sWZC9EOqewqGziZTFb7xCYBIpVKMW3aNPj6+nKmV+oIqX/iBLZkyRL4+fnJY1Vij4+Px/z581FYWCiIqa2kWDY2Npw7VnZ2tiDK9HchZbW1tUVBQQEkEsrmVasIUv/EP2fz5s0YPHgwF6sW+8mTJ7Fu3Tps3LhREC07KRYx9iR7Inh1Ejtp2RcuXIhBgwbBy8uLj6oXpN5nzJiBOXPmYPTo0dVBjir7O1YYfESEZoj93cGDB/lv6knnzp2ZvXv38t8U2N+VlJApnCI0U2V/R/bqTJWmq6izoce0G0ewPewc8mtMJqKT7OSbOPDjNmzesgV7Dp9AWp6iF9cLmIIkhIbuwcWHZLI2vdSJ2KUZFzBz1AhMW/B/eE61RWAlTm9eiF7u7pgQOBOzg4IweYw33HsPx9ZTSfw5QqcMh76ag4kTJ2PPpXen/dKEysVenHEF0yZMQUwaextpYAmtOrt31D13w1fgo9kb8EizI0K2HcKlC6fwzcJxKEk8hlmBk3H0vtANTosRuX4OgtafYD9bw8JAgVcKRahQiuX47dQOjB4wGLsuyFs9DYqFjqK7WB28DmlaLfDtoWgsnT4abu79MG/dARzcOBnaGZewdNVuvPWmd8EgeXEHX88djTGLtoPzj6C6MuWopgSyl9j58Vj0HDAVsfck6NW3Fyz0AEZK74Oc1HM/4+iDcjQbOgl+Pchyhtd4Bc7B4OY6uHv8J1xJF55lQsq5XfDu2QsLvo+FVZuu6NaWLT9Df2dXJWJnSu/hwL+PQurghrWHL+PoN0GwYu94DMWmQonXbkECDfTs0Q1mfKwacye4d20F5N3D5VtP+KBQYHA16gDiH0nhPXM9zp+KwPjuZJUx/SMNKhG7TKMJZv8QgVs34rBo1Puw0ChFKdXXpgCpKc/ZvSEaNiYV/TYmaGzfmN2z5yULTexStPWZjZizN3B8y2do2dgUkhLyBg/6H8qpROzahk4YPskXLW3lk8ikbIv+xvAmfTBFeJFHvAxNYW3xTrvOoglLG3m8MC9foV8OvejgPc+h8PZoy8u7jC2fMJ4+09/rqAvKS5BXTNxu9GCo8NWKGjA0lE+pyMvJAcUvo1ArRLErgr0taVVND62lUZPJ5P0RMo1UGO2e8BHFrghdY1ibEBMgCYokitptBnm58kFHS2sriCsA6EAUu0KMYWNhzu4LkE0csN6hAoX55IGSJkyt6HPGUldEsSvECM2dySp6CTLSFb0epwjpmeTRuRkcHR3kIZF6jyj2WujgKh9fv5hw6d2XKLx8iPhrSYC1C1zfI0OQIjQgir0W7N1HYVQHfaQf24l/hd3jo4RyhH+3ASfTZOg0bBK624vWxLRQZ2Ln1j/RPACt3wLzli1EU2Rihd8ATFvxPaKjDiJ4ymD4rYqATqtBWP25H5vwqAO0V6acuhG7rBxFZCpFsQSVFF+jdiO/xIGf1qFn83Js/3Iuhg4bj9W7zqBlb3/s3b0dA9TCv5JBWQnpjBejtILuefx1InatFt4IOx6N6B8Xo9Hbb4ukDNcJC3Hy/CXExUThyJGjOH72Ks6d2odx3Sm2gfuPMIP/8lBER8dgpqcjH6OTOhG7hlkTeA7ygU+vjjCiewo0h4GtM/p6D8Hw4cMwyKMbrBQ9VBUsunDu1Ac+Pt5oY2/Cx+hE7KCKqA2i2EXUhmqxMwzDzfMwMlKP8QUhQ2zvxLpEtSNcFdUmSTExMVi0aBECAwOhq3CmH30YGxtzhS0upnrV938MMYUKDQ1Fx44duU1dWb9+PWf8NXbsWO57tdgTEhI4XzziovWm1watkGJZWFhw+7y8PEGU6e9CykpaNeIMRuCrWK0gZSa2hxs2bOCc0QjVYj9+/Dj3KyAtvFBuf1WVrE5CJxBzJOJvGBAQgPHjx/NR9cPd3R1BQUGYMGEC9706Zye3PtISkBaBiEMIG8lbufnmCo4JeSN1SJyLCYqOq8tGfvRE11W8MxpTdZFE6KWqDt+saJE6HHo8+d0sDJvzNTKF1DcsTcHyoFEI2nqeDwgXac5D7N24CEP7e6KvV39MXbQJlx+J9nfvkHz6O8z5bCuiYq6iUDDemsX4ec1ChGwJx+k7QnMUqElR6jlM7OeBDz9bj7g7Kch49At2rP8UPd37Ye2xB/xZ9KFysf8a/S18xy/Eo3I2X7Q2g5YQ+oaVrxC6YjqmhoRzX62N9bi9IJGkYU3QJBy8lY2Ri3/EjRvXcf36TURtXgiHrFv4fNYMnEyhc4m5ysRe+Owefgj2w8Bh8/FbNvEZYcXO/ZNmKvH41xOYO9obE7/8CYV8VMgknd+LzbEZaDxgAbauCUBbBxuYN3DEkFnr8O3ykUD6eXzzQzRovGGrRuwVj7DMtx9mrN6PPAd3LFk0C42MWKlU0N1BepF4CKN6eeP7iJtw8fLHwqkDuXilYMetpUiIDEM+20z5+o+BDR+twmfsWLQxAeLjYpBCoaerSsQuK3uGJ1l68PIPxrn4OKz+yAO6ZECA5snsLNkZySgzfw8z1oUi4cQ++Hdvwh8RKMxT/Ebs/DSc0aVdIz74Gi2ntvigiTFK793F/Qz61K6all23HdbFnMepfavg1lQXlUVFoNjmsZrGXSci8sJZbF3oB0stNlUrFrgdUsFzpLxgRazfENamCham6JnD3sKUzeufIyP3nZW59R6ViF1L1xItWjtU5+iUN+jVmFo7wKmZGlll5OXiRYkUaGABWwNFbjimsGlInq7nsafS9xY+lXVQRQSApAj5pOeppQVNDUXDC5rQ0SarcYqQm0Pfu7dEsYu8Rt8QJvzKMvK4/V2kKC0lk8sMYGxK3/CrKHaR15iR9IWVRHY+shXa/hUi+yV5JG4JK2v6FpuLYhd5jbkVGpuzOXlBNnJK5c9KalBZgtxCVuxa1rA1YTuqlCGKXeQ1Gk3h0t6GFfUDPHiczQffIPMJ7j4vABybobmdKHYRqtFDt35e0IYExyLPsxl6TRLPn0BiFoMOrn3QyoY+6YhiF6nB+wMDMLApcG37cnx18AbKuWFkBpm3o7E4+AcU69ghYPJo0GiqUTdiZ2QoJ+9UKpcKwDTtNZUyeVtXLoQnZrWg07A7QjaEoLlOBlaM7w2vUQEICvCFq/tQxKZVYMTSbZje992nqzRQN2LXMUSDhlawsjWHthBmPfLoGpnDysoKNmbyV8wIlfdHL0VsbCim+HRAYsx+bN9/EpqtvbF6zwns/HwYaC19nYhdu+1IXPgjGcnRa9GUbhOpGnSatBHJyckIXzKEjwiXFn38sDMyAWnPXyDrxXPcvRSNJZM8YE6xaXHdtOxaujA1M4OZiSE0BdSya+sZwowtl7GBDh8ROJqkHs1hbm4GIz36rbnFDqqI2iCKXURtqCF20TJNGBD7O4KenoCXD/4NqmxUqqg2STp48CBnquPp6cn5jtAOKVazZs2wdu1anD59GmFhYSgtLUU5NyYqbEjZU1NTuf4FGT1SR8g1iI2NxaZNmzBnzhwuVi32O3fuYN++fVzLTn4NfJhaiEFO06ZNMWXKFFy7dg3x8fGcnwoxglI8o084kPI1btwY+fn53Cb08r4NKS/xzCFlJz6Pbm5u8niV2EVEhI7YQRVRG0Sxi6gNothF1ATg/wHhFTyQTGLDwwAAAABJRU5ErkJggg==" width="122" height="96"></p>
10 Views|Posted 6 months ago
Asked by Shiksha User
The question is closed for answering
1 Answer
P
Answered by
6 months ago
Correct Option - 1
Detailed Solution:
Using truth table of logic gates
Similar Questions for you
A n-p-n transistor can be used as amplifier.
Corresponding binary numbers of given waveforms.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
66K
Colleges
|
1.2K
Exams
|
6.9L
Reviews
|
1.8M
Answers
Learn more about...

Physics Ncert Solutions Class 12th 2026
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
or
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
or
See what others like you are asking & answering