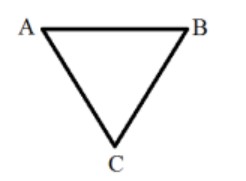
Three thin rods of mass m and length a each are joined to form a triangle ABC in vertical plane. The triangle is pivoted at the vertex A such that it can rotate in the vertical plane. It is released from rest when the side AB is horizontal as shown. As the triangle rotates, the maximum velocity of the vertex B, VMAX , is given by:
Using parallel axis theorem for the side BC, the moment of inertia of the triangle about an axis passing through A and perpendicular to the plane of the triangle, I? = 2 [ (1/3)ma²] + [ (1/12)ma² + m (√3a/2)²] = (3/2)ma² If the angular velocity of the triangle at any instant is ω, the velocity of the
Upvote 
