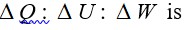Two ideal polyatomic gases at temperatures T₁ and T₂ are mixed so that there is no loss of energy. If F₁ and F₂, m₁ and m₂, n₁ and n₂ be the degrees of freedom, masses, number of molecules of the first and second gas respectively, the temperature of mixture of these two gases is:
Two ideal polyatomic gases at temperatures T₁ and T₂ are mixed so that there is no loss of energy. If F₁ and F₂, m₁ and m₂, n₁ and n₂ be the degrees of freedom, masses, number of molecules of the first and second gas respectively, the temperature of mixture of these two gases is:
U = U? + U? = (n? /N_A) (F? R/2)T? + (n? /N_A) (F? R/2)T?
For the mixture: U = (n? +n? )/N_A * (FR/2)T
F = (n? F? + n? F? ) / (n? + n? )
Equating the expressions for U and solving for T gives:
T = (n? F? T? + n? F? T? ) / (n? F? + n? F? )
Upvote 
Similar Questions for you
From A to B the process is isobaric
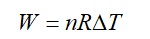
= W = 2 × R (600 - 350)
= 500 R
Heat is path dependent so path function but internal energy does not depend on path chosen.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering