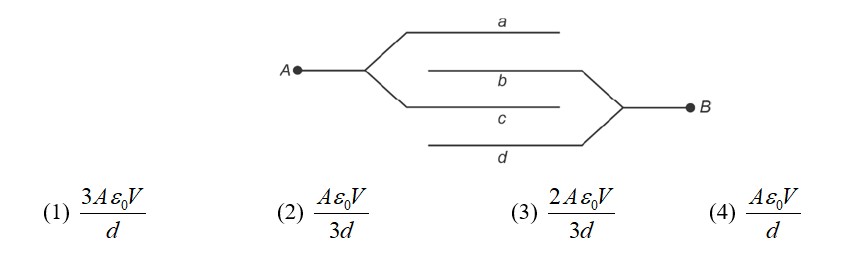
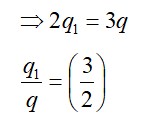Two isolated conducting spheres S₁ and S₂ of radius (2/3)R and (1/3)R have 12µC and -3 µC charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire. A long time after this is done the charges on S₁ and S₂ are respectively:

Option 1 -

+4.5µC and -4.5µC

Option 2 -

4.5µC on both

Option 3 -

6µC and 3µC

Option 4 -

3µC and 6µC

3 Views | Posted a month ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

a month ago

Correct Option - 3

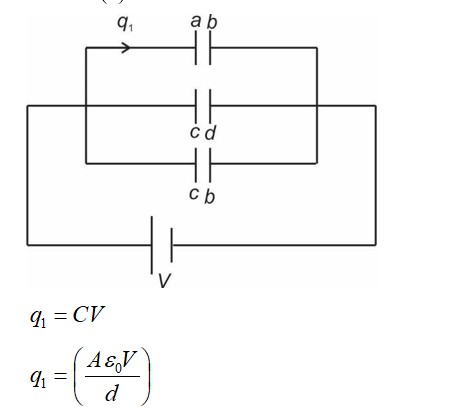
Detailed Solution:

When the two conducting spheres are connected by a wire, they will reach the same electric potential, V.
The total charge Q_total = 12µC + (-3µC) = 9µC. This total charge will redistribute.
Let the final charges be q? and q? + q? = 9µC.
The potential of a sphere is V = kq/r.
V? = V?
k q? /R? = k q? /R? ⇒ q? /R? = q? /R?
q? / (2R/3) = q? / (R/3) ⇒ q? /2 = q? ⇒ q? = 2q?
Substitute this into the charge conservation equation:
2q? + q? = 9µC ⇒ 3q? = 9µC ⇒ q? = 3µC.
Then, q? = 2 * 3µC = 6µC.
The final charges are 6µC and 3µC.

0 Upvotes 0 Downvotes

Similar Questions for you

A parallel plate capacitor is charged and then charging battery is disconnected. If the plates are now pulled apart with insulated handles

alok kumar singh

Charge remains same

Energy stored in circuit 1 is E. If capacitors in circuit 1 and circuit 2 are connected in parallel as shown, the energy stored becomes $\frac{x E}{6}$ , find x.

alok kumar singh

Charge on C₁ = CV

Charge on C₂ = 4CV

When connected in parallel

$V_{C} = \frac{5 V}{3}$

$Q'_{1} = \frac{5}{3} C V$ $Q'_{2} = \frac{10}{3} C V$

$?$ $E = \frac{1}{2} C V^{2}$

$E' = \frac{25}{18} C V^{2} + \frac{25}{9} C V^{2}$

$\frac{25}{6} C V^{2} = \frac{50 E}{6}$

x = 50

Potential due to electric dipole on axial position at distance r from dipole is proportional to (assume r >> length of dipole)

alok kumar singh

$| E | = \frac{2 k P}{r^{3}}$

$E = - \frac{d v}{d r}$ , $v \propto \frac{1}{r^{2}}$

The force between two charged particle placed in air at separation x is F₀. Both the charged particle immerged in a medium of dielectric constant K without changing separation between two charge, then net force on one of the particle is now

alok kumar singh

In air $F = \frac{1}{4 π \in_{0}} \frac{q_{1} q_{2}}{r^{2}}$

In medium $F' = \frac{1}{4 π (k \in_{0})} \frac{q_{1} q_{2}}{r^{2}}$

$F' = \frac{F_{0}}{K}$

Five metallic plates each of area A and separated from adjacent plate by a distance d as shown in figure. The capacitance of the system across A and B is: