Ask & Answer: India's Largest Education Community
All Questions
New Question
5 months agoContributor-Level 10
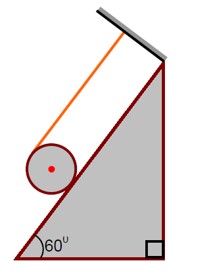
μ_min = (I tanθ)/ (I + mR²)
= [ (mR²/2)tanθ] / [mR²/2 + mR²] = (tanθ)/3 = (tan 60°)/3 = √3/3 = 1.732/3 = 0.5773
Since given coefficient of static friction is less than μ_min, so body will perform rolling with slipping and kinetic friction will act
F? = μN = μmg cosθ = (0.4) × mg cos 60° = mg/5
New Question
5 months agoContributor-Level 10
SDJ International College has top-notch infrastructure, which is equipped with all the necessary amenities. The college has spacious and ventilated classrooms with state-of-the-art visual aids, internet and intranet connectivity with hi-tech multimedia and audiovisual equipment. The college has 10000+ books by renowned authors and publications to enrich the knowledge of our students. SDJ International College has CCTV surveillance, 24*7 communication, fire safety, uninterrupted power, structure stability, and others.
New Question
5 months agoContributor-Level 10
Let x = m(a + λb).
Given m(a + λb) ⋅ (3i + 2j - k) = 0, which leads to λ = -3/8.
The projection of vector x on vector a is given by x ⋅ â, where â is the unit vector of a.
Projection = (x ⋅ a) / |a| = 17√6 / 2
x ⋅ a = (m(a + λb)) ⋅ a = m(a ⋅ a + λ(b ⋅ a)) = m(|a|^2 + λ(b ⋅ a))
The provided text simplifies this to:
m(6 - 3/8 * (-1)) = 17√6 / 2
m * (51/8) = 17 * 6 / 2 (The text seems to have a typo 17x6/2 instead of 17√6 / 2)
Assuming it is 17 * 6 / 2, m * 51/8 = 51, so m = 8.
x = 8(a + (-3/8)b) = 8a - 3b
x = 8( (13/8)i - (14/8)j + (11/8
New Question
5 months agoContributor-Level 10
As we know that direction of propagation of electromagnetic wave is perpendicular to plane containing mutually perpendicular electric field and magnetic field, so option D will be correct answer.
New Question
5 months agoContributor-Level 10
The problem provides an equation involving the coordinates (α, β, γ) of a point P:
((α + β + γ) / √3)^2 + ((α - nγ) / √(l^2 + n^2))^2 + ((α - 2β + γ) / √6)^2 = 9
The locus of P(α, β, γ) is given by replacing (α, β, γ) with (x, y, z):
((x + y + z) / √3)^2 + ((lx - nz) / √(l^2 + n^2))^2 + ((x - 2y + z) / √6)^2 = 9
This represents the equation of an ellipsoid. The text proceeds by comparing coefficients. By expanding the equation, the coefficients of x^2, y^2, z^2, and cross-product terms are collected. From the
New Question
5 months agoContributor-Level 10
Candidates with a valid BPharm degree of Uttar Pradesh University of Medical Sciences are eligible for job roles in the government sector. There are various central and state government organisations that post job opportunities for Pharmacy degree holders. Some of the popular job profiles for BPharm candidates are TSPSC Drug Inspector, MPSC Pharmacist, ESIC Pharmacist, SBI Pharmacist, etc.
New Question
5 months agoContributor-Level 10
Some of the top colleges that provide a good ROI when it comes to BCA courses are Christ University, SICSR Pune, Loyola College, Stella Maris, and MCC Chennai. Other strong alternatives that could be considered are Kristu Jayanti and Amity Noida. For a more detailed outlook on the BCA course and its colleges, you can refer to : BCA course complete overview.
New Question
5 months agoContributor-Level 10
If the orthocenter and circumcenter of a triangle both lie on the y-axis, the centroid also lies on the y-axis.
The x-coordinate of the centroid is (x1 + x2 + x3) / 3. If the vertices are (cos α, sin α), (cos β, sin β), (cos γ, sin γ), then the x-coordinate of the centroid is (cos α + cos β + cos γ) / 3.
Since the centroid lies on the y-axis, its x-coordinate is 0.
cos α + cos β + cos γ = 0
Using the identity: If a + b + c = 0, then a^3 + b^3 + c^3 = 3abc.
Let a = cos α, b = cos β, c = cos γ.
Then, cos^3 α + cos^3 β + cos^3 γ = 3 * cos &alph
New Question
5 months agoBeginner-Level 1
The eligibility criteria for the BA programs at AAFT Noida For quite straightforward and student-friendly. Candidates must have passed 10+2 or a equivalent examination from a recognised board in any stream. Admissions are generally based on the AAFT Global Entrance Exam (GEE) followwed by a personal interviw, which helps evaluate a student's creativity and communication skills rather than just academic scores.
For most BA specializations, a minimum of 45–50% marks in 10+2 is preferred. What makes AAFT stand out is its industry-oriented approach — students get practical exposure, modern facilities, and opportunities to work on live p
New Question
5 months agoNew Question
5 months agoContributor-Level 10
The numbers 1, log10(4^x - 2), and log10(4^x + 18/5) are in an Arithmetic Progression (A.P.).
This means that the corresponding numbers 10^1, 10^(log10(4^x - 2)), and 10^(log10(4^x + 18/5)) are in a Geometric Progression (G.P.).
So, 10, 4^x - 2, and 4^x + 18/5 are in G.P.
For a G.P., the square of the middle term is equal to the product of the other two terms:
(4^x - 2)^2 = 10 * (4^x + 18/5)
Let y = 4^x.
(y - 2)^2 = 10y + 36
y^2 - 4y + 4 = 10y + 36
y^2 - 14y - 32 = 0
(y - 16)(y + 2) = 0
So, y = 16 or y = -2.
Since y = 4^x, y must be positive. Thus, 4^x = 16, which gives x = 2.
The determinant calculation that follows appears to be unrelated to the
New Question
5 months agoContributor-Level 10
z = √ [R² + (X? - X? )²] = √ [6² + (4-10)²] = 6√2 Ω
Power factor = cosφ = R/z = 6/ (6√2) = 1/√2
New Question
5 months agoContributor-Level 10
Given matrices A = [[a, b], [c, d]] and B = [[α], [β]] where B ≠ [[0], [0]].
The product AB is:
AB = [[a, b], [c, d]] * [[α], [β]] = [[aα + bβ], [cα + dβ]]
From the problem statement AB = B, we have:
aα + bβ = α (i)
cα + dβ = β (ii)
Rearranging these equations:
(a - 1)α + bβ = 0
cα + (d - 1)β = 0
For this system of linear equations to have a non-trivial solution (since B is not the zero matrix), the determinant of the coefficient matrix must be zero.
det([[a-1, b], [c, d-1]]) = 0
(a - 1)(d - 1) - bc = 0
ad - a - d + 1 - bc = 0
ad - bc = a + d - 1
Th
New Question
5 months agoNew Question
5 months agoContributor-Level 10
BA programme at AAFT is a full-time three-year undergraduate course structured across six semesters. The programme is designed to provide students with strong theoretical foundations and practical training in their chosen field. In three years, students get hands-on exposure industry interactions and opportunities to build a professional portfolio for career growth.
New Question
5 months agoContributor-Level 10
Given the integral In = ∫(log|x|)^n / x^19 dx.
Let t = log|x|, which implies x = e^t and dx = e^t dt.
The integral becomes:
In = ∫ e^(-20t) * t^n dt
Using integration by parts, where u = t^n and dv = e^(-20t) dt:
In = [t^n * e^(-20t) / -20] - ∫ n*t^(n-1) * e^(-20t) / -20 dt
In = e^(-20) / -20 - (n / -20) * In-1
20 * In = -e^(-20) + n * In-1
For n = 10: 20 * I10 = e^20 - 10 * I9 (Note: There seems to be a sign inconsistency in the original document's derivation vs. standard integration by parts, the document states e^20 instead of -e^(-20) and proceeds with e^20).
For n = 9: 20 * I9 = e^20 - 9 * I8
From these two equations, we can exp
New Question
5 months agoContributor-Level 10
With the help of definition of e, we can write
e = v? /v? = 2v/u ⇒ u = 2v/e . (2)
Putting the value of e in equation (1), we have
m? (2v/e) = (m? - m? )v ⇒ 2m? = em? - em? ⇒ m? /m? = (2+e)/e = 1 + 2/e > 2
New Question
5 months agoContributor-Level 9
Yes, UPUMS offers a four-year BPharm course at the undergraduate level. It is provided through the faculty of Pharmacy of the university. Candidates can get admission based on merit in the CPNET, conducted by the university. For eligibility, the minimum requirement is that the candidate must be Class 12 or equivalent exam pass. The eligible students can go to the official website to apply.
New Question
5 months agoRegister to get relevant
Questions & Discussions on your feed
Ask & Answer
Panel of Experts