Ask & Answer: India's Largest Education Community
All Questions
New Question
5 months agoContributor-Level 9
Bohr's theory accounts for the line spectrum of single electron species but Li? has two electrons. Bohr's theory fails to explain splitting of spectral lines in presence of magnetic field i.e. Zeeman effect.
New Question
5 months agoContributor-Level 10
To find the sum Σ[r=0 to 6] (?C?)².
This is the coefficient of x? in the expansion of (1+x)?(x+1)? = (1+x)¹².
By the binomial theorem, (1+x)¹² = Σ[k=0 to 12] ¹²C? x?.
The coefficient of x? is ¹²C?.
¹²C? = (12 * 11 * 10 * 9 * 8 * 7) / (6 * 5 * 4 * 3 * 2 * 1) = 11 * 2 * 3 * 2 * 7 = 924.
New Question
5 months agoContributor-Level 10
I? = I? + I? ⇒ I? /I? = 1 + I? /I? ⇒ 1/α = 1 + 1/β = (β+1)/β ⇒ α = β/ (1+β)
⇒ 1/β = 1/α - 1 = (1-α)/α ⇒ β = α/ (1-α)
New Question
5 months agoContributor-Level 10
IIT Palakkad JEE Advanced cutoff 2025 for BTech admission ranged between 5736 and 16753 for the General AI category students. This is overall cutoff range, including all six rounds for BTech. The cutoff range differs for different rounds and categories. Considering 2025 cutoff ranks BTech in CSE had lowest rank of 5736 in first round and 6454 during last round of admission. Students can refer to the table below to view IIT Palakkad branch-wise cutoff 2025 for both the first and last rounds.
| Course | Round 1 Closing Rank 2025 | Last Round Closing Rank 2025 |
|---|---|---|
| B.Tech. in Civil Engineering | 14852 | 16753 |
| B.Tech. in Computer Science and Engineering | 5736 | 6454 |
| B.Tech. in Electrical Engineering | 9210 | 10396 |
| B.Tech. in Mechanical Engineering | 11216 | 12606 |
| B.Tech. in Data Science and Engineering | 7559 | 8640 |
New Question
5 months agoContributor-Level 10
g? = g - ω²R ⇒ 0 = g - ω²R ⇒ ω = √ (g/R)
⇒ T = 2π/ω = 2π√ (R/g) = 2 × 3.14 × √ (6400 × 10³)/10)
New Question
5 months agoContributor-Level 10
I = ∫[0 to 10] [sin(2πx)] / e^(x-[x]) dx.
The period of the integrand involves [sin(2πx)] which depends on the sign of sin(2πx) and {x} = x - [x], which has a period of 1.
Let f(x) = [sin(2πx)] / e^{x}.
The integral is ∫[0 to 10] f(x) dx = 10 * ∫[0 to 1] f(x) dx due to the periodicity of {x} and the integer period of sin(2πx).
In the interval (0, 1/2), sin(2πx) is between 0 and 1, so [sin(2πx)] = 0.
In the interval (1/2, 1), sin(2πx) is between -1 and 0, so [sin(2πx)] = -1.
At x=0, 1/2, 1, the value is 0.
So, ∫[0 to 1] f(x) dx = ∫[0 to 1/2] 0 dx + ∫[1/2 to 1] -1/e^x dx
= 0 + [-e^(-x) * (-1)] f
New Question
5 months agoContributor-Level 10
(A) sin (ωt) + cos (ωt) = √2 sin (ωt + π/4) ⇒ T = 2π/ω
(B) sin² (ωt) = 1/2 - (1/2)cos (2ωt) ⇒ T = 2π/ (2ω) = π/ω
(C) 3cos (π/4 - 2ωt) ⇒ T = 2π/ (2ω) = π/ω
(D) cos (ωt) + cos (2ωt) + cos (3ωt)
Time period of cos (ωt) = 2π/ω
Time period of cos (2ωt) = 2π/ (2ω)
Time period of cos (3ωt) = 2π/ (3ω)
Time period of combined function = 2π/ω
New Question
5 months agoContributor-Level 10
Find the number of solutions for 2tan(x) = π/2 - x in [0, 2π].
This is equivalent to finding the number of intersection points of the graphs y = tan(x) and y = (π/4) - x/2.
Let's sketch the graphs:
y = tan(x) has vertical asymptotes at x = π/2, 3π/2.
y = (π/4) - x/2 is a straight line with a negative slope.
At x=0, y=π/4.
At x=π/2, y=0.
At x=π, y=-π/4.
At x=2π, y=-3π/4.
By observing the graphs, there will be one intersection in (0, π/2), one in (π/2, 3π/2), and one in (3π/2, 2π].
Total number of solutions is 3.
New Question
5 months agoContributor-Level 10
Last date to apply for NCHM JEE exam 2025 was 15th January 2025. The registrations for the exam started from 16th December 2024. The NCHM JEE 2025 exam was held on 27th April 2025.
New Question
5 months agoContributor-Level 10
A = Area swept ⇒ dA/dt = (1/2)r² (dθ/dt) = (1/2) (Mr²ω)/M = L / (2M)
New Question
5 months agoContributor-Level 10
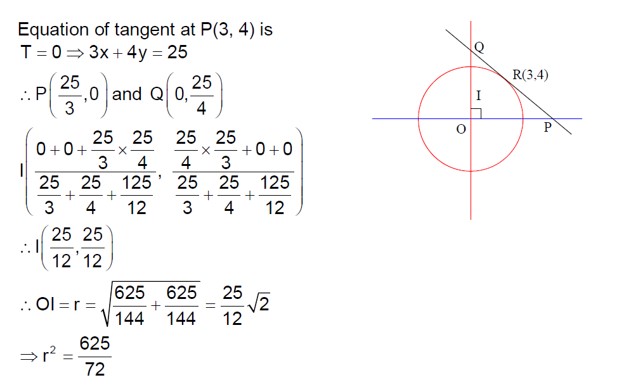
Parabola: y² = 4x - 20 = 4(x - 5). Vertex at (5,0).
Line: The text seems to derive the tangent equation y = x - 4. This is not a tangent to the given parabola. The standard tangent to y²=4aX is Y=mX+a/m. Here X=x-5, a=1. So y = m(x-5)+1/m.
The other curve is an ellipse: x²/a² + y²/b² = 1.
The text says x²/2 + (x-4)²/b² = 1. This assumes a² = 2.
x²/2 + (x²-8x+16)/b² = 1
x²(1/2 + 1/b²) - (8/b²)x + (16/b² - 1) = 0.
For tangency, the discriminant (D) of this quadratic equation must be zero.
D = (8/b²)² - 4(1/2 + 1/b²)(16/b² - 1) = 0.
64/b? - 4(
New Question
5 months agoContributor-Level 10
θ? > I = θ ⇒ sinθ? > sinθ ⇒ 1/μ > sinθ
⇒ μ < 1/sinθ
Note: If we assume θ = 45° ⇒ μ < 1.414, then red colour light ray will come out from face PR of prism.
New Question
5 months agoContributor-Level 10
No, the BSc admissions at IHM, Ahmedabad for the year 2025 have now been closed. Candidates need to appear for the NCHM JEE exam to gain admissions at IHM, Ahmedabad BSc courses. The NCHM JEE 2025 exam has been concluded. Candidates who appeared for the exam have already received the results of their exam performance. The dates for the NCHM JEE 2026 will be announced soon.
New Question
5 months agoContributor-Level 10
Given that x, y, z are in A.P., so 2y = x + z.
The determinant is:
| 3 4√2 x |
| 4 5√2 y | = 0
| 5 k z |
Apply the operation R? → R? + R? - 2R?:
The first row becomes:
(3 + 5 - 24) (4√2 + k - 25√2) (x + z - 2y)
= 0 (k - 6√2) (0)
So the determinant becomes:
| 0 k-6√2 0 |
| 4 5√2 y | = 0
| 5 k z |
Expanding along the first row:
-(k - 6√2)(4z - 5y) = 0.
This implies k - 6√2 = 0 or 4z - 5y = 0.
k = 6√2 or y = 4z/5.
The condition y = 4z/5 is stated as not possible.
Therefore, k = 6√2, which means k² = (6√2)² = 36 * 2 = 72.
New Question
5 months agoContributor-Level 10
PV? = C ⇒ V? (dP/dV) + P (γV^ (γ-1) = 0 ⇒ dP/dV = -γ (P/V) ⇒ dP/P = -γ (dV/V)
New Question
5 months agoContributor-Level 10
U = mV (r) = -Cm/r
F = -dU/dr = -Cm/r² ⇒ The force which provides required centripetal force
⇒ mv²/r = Cm/r² ⇒ r = C/v²
New Question
5 months agoContributor-Level 10
NCHM JEE is compulsory for every candidate who wishes to take admissions into the IHM, Ahmedabad BSc exams. The last date to register for the exam is Jan 2025, 2026. The exam is scheduled to take place 25th April 2026.
New Question
5 months agoContributor-Level 10
The institution offers good placements to its PG and UG graduating students. The overall key highlights of Thiagarajar College of Engineering placements 2025 as compared with 2024 and 2023 are presented below:
Particulars | Placement Statistics (2023) | Placement Statistics (2024) | Placement Statistics (2025) |
|---|---|---|---|
the highest Package | INR 32 LPA | INR 21 LPA | INR 29 LPA |
Average Package | INR 7 LPA | INR 7.25 LPA | INR 7.1 LPA |
Students Placed | 761 | 669 | 809 |
Register to get relevant
Questions & Discussions on your feed
Ask & Answer
Panel of Experts