Is Class 12th Math Inverse Trigonometric Functions NCERT Solutions important for Boards exams?

  $f\left(x\right)=e^{x^3-3x+1}$

$f\text{'}\left(x\right)=e^{x^3-3x+1}$  (3x² − 3)

$e^{x^3-3x+1}$ = ⋅ 3(x −1)(x +1)

For x ∈ (−∞, −1], f '(x) ≥ 0

∴     f(x) is increasing function

∴     a = e^–∞ = 0 = f (−∞)

b = e⁻¹⁺³⁺¹ = e³ = f (−1)

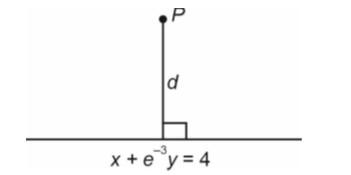
∴     P(4, e³ + 2)

$d=\frac{\left(e^3+2\right)\left(e^{-3}\right)}{\sqrt[]{1+e^{-6}}}=\frac{1+2e^{-3}}{\sqrt[]{1+e^{-6}}}=\frac{1+2e^{-3}}{\sqrt[]{1+e^{-6}}}=\frac{e^3+2}{\sqrt[]{e^6+1}}$

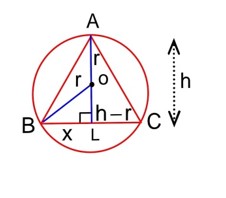
From option let it be isosceles where AB = AC then

$x=\sqrt[]{r^2-{\left(h-r\right)}^2}$            

 =   $\sqrt[]{r^2-h^2-r^2+2rh}$

$x=\sqrt[]{2hr-h^2}........\left(i\right)$        

Now ar $\left(\Delta ABC\right)=\Delta =\frac{1}{2}BC\times AL$

$\Delta =\frac{1}{2}\times 2\sqrt[]{2hr-a^2}\times h$       

then   $x=\sqrt[]{2\times \frac{3r}{2}\times r-\frac{9r^2}{4}}=\frac{\sqrt[]{3}}{2}rfrom\left(i\right)$

$\Rightarrow BC=\sqrt[]{3}r$      

So . $AB=\sqrt[]{h^2+x^2}=\sqrt[]{\frac{9r^2}{4}+\frac{3r^2}{4}}=\sqrt[]{3}r$

Hence $\Delta$ be equilateral having each side of length $\sqrt[]{3}r.$  

$g\left(2\right)=\underset{x\to 2}{lim}g\left(x\right)=\underset{x\to 2}{lim}\frac{x^2-x-2}{2x^2-x-6}=\underset{x\to 2}{lim}\frac{\left(x-2\right)\left(x+1\right)}{2x\left(x-2\right)+3\left(x-2\right)}$           

$Nowfog=f\left(g\left(x\right)\right)=si{n}^{-1}g\left(x\right)=si{n}^{-1}\left(\frac{x^2-x-2}{2x^2-x-6}\right)$

$\frac{3x^2-2x-8}{2x^2-x-6}\ge 0\&\frac{-x^2+4}{2x^2-x-6}\le 0$          

On solving we get   $x\in \left(-\infty ,-2\right)\cup \left[\frac{-4}{3},\infty \right)$

As x = 2 also lies in domain since g(2) $=\underset{x\to 2}{lim}g\left(x\right)$  

$f\left(x\right)=2co{s}^{-1}x+4co{t}^{-1}x-3x^2-2x+10\forall x\in \left[-1,1\right]$

$\Rightarrow f\text{'}\left(x\right)=-\frac{2}{\sqrt[]{1-x^2}}-\frac{4}{1+x^2}-6x-2<0\forall x\in \left[-1,1\right]$

So, f (x) is decreasing function and range of f (x) is

$\left[f\left(1\right),f\left(-1\right)\right],$ which is $\left[\pi +5,5\pi +9\right]$

Now 4a – b = 4 (p + 5) - (5p + 9) = 11 - “π”

$g\left(f\left(x\right)\right)=x\Rightarrow g\text{'}\left(f\left(x\right)\right).f\text{'}\left(x\right)=1$

$f\left(x\right)=1\Rightarrow x=0$

$g\text{'}\left(1\right).f\text{'}\left(0\right)=1$

$f\text{'}\left(x\right)=2x+e^{-x}$

$\begin{array}{l}f\text{'}\left(0\right)=1\\ g\text{'}\left(1\right)=1\end{array}$