1. Show that 9n+1– 8n – 9 is divisible by 64, whenever n is a positive integer.

1. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9n+1 – 8n – 9 to be divisible by 64 we need to show that 9n+1 – 8n – 9 = 64k where k is some natural number. We have, by binomial theorem (1 + a)m = mC0 + mC1 (a) + mC2 (a)2 + mC3 (a)3 + ………… + mCm (a)m Putting, a = 8 and m = n + 1 (1 + 8)n+1 = n+1C0 + n+1C1.8 + n+1C2.82 + n+1C3.83 + ……. + n+1Cn+1. (8)n+1 => 9n+1= 1 + (n + 1)8 + 82* [n+1C2 + n+1C3.8 + ………. + n+1Cn+1. (8)n+1–2] [since, n+1C0 = 1, n+1C1= n + 1] => 9n+1 = 1 + 8n + 8 + 64 * [n+1C2 + n+1C3.8 + ………. + n+1Cn+1. (8)n+1-2] => 9n+1 – 8n – 9 = 64 * [n+1C2 + n+1C3.8 + ………. + 8n–1] [since, n+1Cn+1 = 1] => 9n+1 – 8n – 9 = 64k, where k = n+1C2 + n+1C3.8 + ………. + 8n–1 is a natural number. This shows that 9n+1 – 8n – 9 is divisible by 64

1. Show that 9ⁿ⁺¹– 8n – 9 is divisible by 64, whenever n is a positive integer.

287 Views|Posted 9 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Payal Gupta | Contributor-Level 10

9 months ago

1. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9ⁿ⁺¹ – 8n – 9 to be divisible by 64 we need to show that 9ⁿ⁺¹ – 8n – 9 = 64k where k is some natural number.

We have, by binomial theorem

(1 + a)^m = ^mC₀ + ^mC₁ (a) + ^m

Upvote

Similar Questions for you

If ²⁰C_r is the co-efficient of x^r in the expansion of (1 + x)²⁰, then the value of $\sum_{r = 0}^{20} r^{2}$ ²⁰C_r is equal to

Vishal Baghel

Kindly consider the following figure

If the coefficient of x¹⁰ in the binomial expansion of ${(\frac{\sqrt[]{x}}{5^{\frac{1}{4}}} + \frac{\sqrt[]{5}}{x^{\frac{1}{3}}})}^{60}$ is $5^{k} . l,$ where $l, k \in N a n d l$  is co-prime to 5, then k is equal to………...

Alok Kumar Singh

$T_{r + 1} =^{60} C_{r} {(x^{\frac{1}{2}})}^{60 - r} {(x^{- \frac{1}{3}})}^{r} {(5^{\frac{- 1}{4}})}^{60 - r} {(5^{\frac{1}{2}})}^{r}$

for

$x^{10} \frac{60 - r}{2} - \frac{r}{3} = 10$

$\Rightarrow 180 - 3 r - 2 r = 60$

->r = 24

k = 3 + exponent of 5 in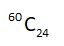

= $3 + ([\frac{60}{5}] + [\frac{60}{5^{2}}] - [\frac{24}{5}] - [\frac{24}{5^{2}}] - [\frac{36}{5}] - [\frac{36}{5^{2}}])$

= 3 + (12 + 2 – 4 – 0 – 7 – 1)

= 3 + 2 = 5

Payal Gupta

15. ${[3 x^{2} - 2 a x + 3 a^{2}]}^{3}$

= ${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

We know that by binomial theorem,

${(a + b)}^{3}$ = $a^{3} + b^{3} + 3 a b (a + b)$

= $a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Then,

${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

= (3x²)³ + ${[a (- 2 x + 3 a)]}^{3}$ + $[3 (3 x^{2})^{2} a (- 2 x + 3 a)]$ + $[3 (3 x^{2}) {a (- 2 x + 3 a)}^{2}]$

= 27x⁶ + $[a^{3} {(- 2 x + 3 a)}^{3}]$ + $[3 (9 x^{4}) (- 2 a x + 3 a^{2})]$ + $[3 (3 x^{2}) {a^{2} {(3 a - 2 x)}^{2}}]$

= 27x⁶ + $[a^{3} {- 8 x^{3} + 27 a^{3} + 3 (4 x^{2}) (3 a) + 3 (- 2 x) (9 a^{2})}]$ + $[- 54 a x^{5} + 81 a^{2} x^{4}]$ + [ $(9 a^{2} x^{2})$ $(9 a^{2} + 4 x^{2} - 12 a x)$ ]

= 27x⁶ + [ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ ] + [ $- 54 a x^{5} + 81 a^{2} x^{4}$ ] + [ $(81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$ ]

= 27x⁶ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ $- 54 a x^{5} + 81 a^{2} x^{4}$ + $81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$

= 27x⁶– 54ax⁵ $+ 117 a^{2} x^{4}$ $- 116 a^{3} x^{3}$

Payal Gupta

15. ${[3 x^{2} - 2 a x + 3 a^{2}]}^{3}$

= ${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

We know that by binomial theorem,

${(a + b)}^{3}$ = $a^{3} + b^{3} + 3 a b (a + b)$

= $a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Then,

${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

= (3x²)³ + ${[a (- 2 x + 3 a)]}^{3}$ + $[3 (3 x^{2})^{2} a (- 2 x + 3 a)]$ + $[3 (3 x^{2}) {a (- 2 x + 3 a)}^{2}]$

= 27x⁶ + $[a^{3} {(- 2 x + 3 a)}^{3}]$ + $[3 (9 x^{4}) (- 2 a x + 3 a^{2})]$ + $[3 (3 x^{2}) {a^{2} {(3 a - 2 x)}^{2}}]$

= 27x⁶ + $[a^{3} {- 8 x^{3} + 27 a^{3} + 3 (4 x^{2}) (3 a) + 3 (- 2 x) (9 a^{2})}]$ + $[- 54 a x^{5} + 81 a^{2} x^{4}]$ + [ $(9 a^{2} x^{2})$ $(9 a^{2} + 4 x^{2} - 12 a x)$ ]

= 27x⁶ + [ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ ] + [ $- 54 a x^{5} + 81 a^{2} x^{4}$ ] + [ $(81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$ ]

= 27x⁶ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ $- 54 a x^{5} + 81 a^{2} x^{4}$ + $81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$

= 27x⁶– 54ax⁵ $+ 117 a^{2} x^{4}$ $- 116 a^{3} x^{3}$

Payal Gupta

14. For (a – b) to be a factor of aⁿ – b ⁿwe need to show (aⁿ – bⁿ) = (a – b)k as k is a natural number.

We have, for positive n

aⁿ = ${(a - b + b)}^{n}$ = ${[(a - b) + b]}^{n}$

=>aⁿ = ⁿC₀(a – b)ⁿ + ⁿC₁(a – b)^{n -}¹b + ⁿC₂(a – b)^{n –}²b² + ………… +ⁿC_n_-1 $(a - b) b^{n - 1}$ + ⁿC_nbⁿ

=>aⁿ= ${(a - b)}^{n}$ + ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿC₂ ${(a - b)}^{n - 2} b^{2}$ + …………….…+ ⁿC_n_-1 $(a - b) b^{n - 1}$ + $b^{n}$ [Since, ⁿC₀ = 1 and