26. Find the area enclosed between the parabola y2 = 4ax and the line y = mx
26. Find the area enclosed between the parabola y2 = 4ax and the line y = mx
-
1 Answer
-
The equation of the parabola is -----------(1)
and that of line is ------(2)
The Point of intersection of(1)and (2) is given by
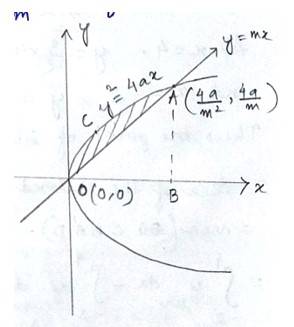
For, i.e, O(0,0)
For, (in first quadrant)
i.e,
Hence, the required area enclosed by the curve and the lines is

Similar Questions for you
differentiating w.r.to x
After solving we get also curve passes through (3, 3) Þ c = -2
which passes through
Since a is a odd natural number then
Þ a = 5
lim (x→∞) (∫? ^ (√x²+1) tan? ¹t dt) / x = lim (x→∞) (tan? ¹ (√x²+1) * (x/√ (x²+1) = lim (x→∞) (tan? ¹ x) * (x/√ (x²+1) = π/2
A = ∫? ² lnx dx = 2ln2 – 1
A' = 4 - 2 (2ln2 – 1) = 6 – 4ln2
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
