31. Using the method of integration, find the area enclosed by the curve |x| + |y| = 1
[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]
31. Using the method of integration, find the area enclosed by the curve |x| + |y| = 1
[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]
-
1 Answer
-
Given equation of the curve is , which can be break down into each quadrant .
For Ist quadrant,
i.e., - (1)
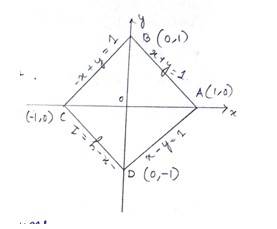
Similarly for IInd, IIIRd nad IVth quadrant
- (2)
- (3)
- (4)
We draw the above focus lines on a graph and find the area enclosed which is a square.
Required area .
Similar Questions for you
differentiating w.r.to x
After solving we get also curve passes through (3, 3) Þ c = -2
which passes through
Since a is a odd natural number then
Þ a = 5
lim (x→∞) (∫? ^ (√x²+1) tan? ¹t dt) / x = lim (x→∞) (tan? ¹ (√x²+1) * (x/√ (x²+1) = lim (x→∞) (tan? ¹ x) * (x/√ (x²+1) = π/2
A = ∫? ² lnx dx = 2ln2 – 1
A' = 4 - 2 (2ln2 – 1) = 6 – 4ln2
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
