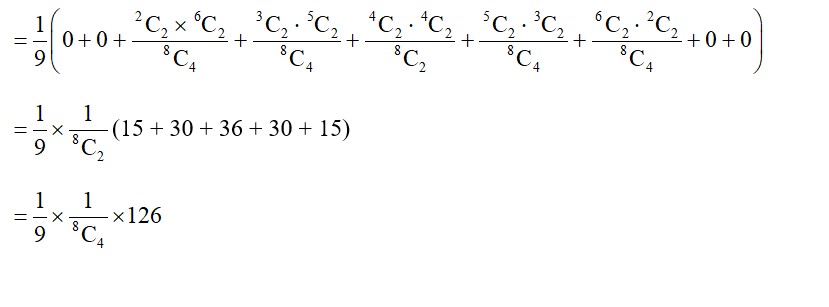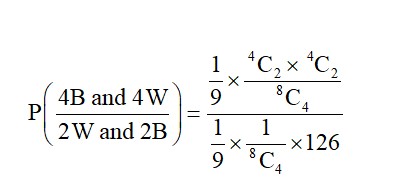Ask & Answer Question

Probability Ncert Solutions Maths class 12th Maths Class 12th Probability

44. Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4 she tosses a coin once and noted whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 and 4 with the die?

2 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

4 months ago

44. Let, $E_{1} :$ event that outcome on the die is $5$ or $6$

$E_{2} :$ event that outcome on the die is $1, 2, 3$ or $4$

$A :$ event of getting exactly one head

$P (E_{1}) = \frac{2}{6} = \frac{1}{3}$

$P (E_{2}) = \frac{4}{6} = \frac{2}{3}$

$P (A / E_{1}) =$ probability of getting exactly one head by tossing the coin three times if she gets $5$ or $6$ $= \frac{3}{8}$

$P (A / E_{2}) =$ probabilit7y of getting exactly one head by tossing the coin three times if she gets $1, 2, 3$ or $4$ $= \frac{1}{2}$

Therefore, by Baye’s theorem,

$P (E_{2} / A) =$ probability that the girl threw $1, 2, 3$ or $4$ with die, if she obtained exactly one head,

$P (E_{2} / A) = \frac{P (E_{2}) . P (A / E_{2})}{P (E_{1}) . P (A / E_{1}) + P (E_{2}) . P (A / E_{2})}$

$= \frac{\frac{2}{3} \times \frac{1}{2}}{\frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{1}{2}}$

$= \frac{\frac{2}{6}}{\frac{3}{24} + \frac{1}{3}} = \frac{\frac{1}{3}}{\frac{3 + 8}{24}}$

$= \frac{1}{3} \times \frac{24}{10} = \frac{8}{11}$

0 Upvotes 0 Downvotes

Similar Questions for you

Let a die rolled till 2 is obtained. The probability that 2 obtained on even numbered toss is equal to

alok kumar singh

P (2 obtained on even numbered toss) = k (let)

P (2) = $\frac{1}{6}$

P ( $\bar{2}$ )= $\frac{5}{6}$

$k = \frac{5}{6} \times \frac{1}{6} + {(\frac{5}{6})}^{3} \times \frac{1}{6} + {(\frac{5}{6})}^{5} \times \frac{1}{6} + . . .$

$= \frac{\frac{5}{6} \times \frac{1}{6}}{1 - {(\frac{5}{6})}^{2}}$

$= \frac{5}{11}$

Given set S = {0, 1, 2, 3, ….., 10}. If a random ordered pair (x, y) of elements of S is chosen, then find probability that |x – y| > 5

alok kumar singh

If x = 0, y = 6, 7, 8, 9, 10

If x = 1, y = 7, 8, 9, 10

If x = 2, y = 8, 9, 10

If x = 3, y = 9, 10

If x = 4, y = 10

If x = 5, y = no possible value

Total possible ways = (5 + 4 + 3 + 2 + 1) * 2

= 30

Required probability $= \frac{30}{11 * 11} = \frac{30}{121}$

A bag contains 8 balls (black and white). If four balls are chosen without replacement then 2W and 2B are found then the probability that number of white and black balls are same in bag is equal to

alok kumar singh

P (2W and 2B) = P (2B, 6W) × P (2W and 2B)

+ P (3B, 5W) × P (2W and 2B)

+ P (4B, 4W) × P (2W and 2B)

+ P (5B, 3W) × P (2W and 2B)

+ P (6B, 2W) × P (2W and 2B)

(15 + 30 + 36 + 30 + 15)

$= \frac{36}{126}$

$= \frac{18}{63}$

$= \frac{6}{21}$

$= \frac{2}{7}$

A coin is biased such that head has two chances than tails, what is the probability of getting 2 heads and 1 tail?

alok kumar singh

Let probability of tail is $\frac{1}{3}$

⇒ Probability of getting head = $\frac{2}{3}$

∴ Probability of getting 2 heads and 1 tail

$= (\frac{2}{3} \times \frac{2}{3} \times \frac{1}{3}) \times 3$

$= \frac{4}{27} \times 3$

$= \frac{4}{9}$

The coefficients a, b and c of the quadratic equation, ax² + bx + c = 0 are obtained by throwing a dice three times. The probability that this equation has equal roots is:

Vishal Baghel

ax² + bx + c = 0

D = b² – 4ac

D = 0

b² – 4ac = 0

b² = 4ac

(i) AC = 1, b = 2 (1, 2, 1) is one way

(ii) AC = 4, b = 4

$\begin{array}{l} a = 4 c = 1 \\ a = 2 c = 2 \\ a = 1 c = 4 \end{array}} 3 w a y s$

(iii) AC = 9, b = 6, a = 3, c = 3 is one way

1 + 3 + 1 = 5 way

Required probability = $\frac{5}{216}$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question