Feedback
×Thank you for using Shiksha Ask & Answer
We hope you got a satisfactory answer to your question.
How likely is it that you would recommend Shiksha Ask & Answer to a friend or colleague?
Not at all likely
Extreme likely
Please suggest areas of improvement for us
76. Find the local maxima and local minima, if any, of the following functions.
Find also the local maximum and the local minimum values, as the case may be:
(i) f(x) = x2.
76. Find the local maxima and local minima, if any, of the following functions.
Find also the local maximum and the local minimum values, as the case may be:
(i) f(x) = x2.
-
1 Answer
-
(i) we have, f(x) = x2.
f(x) = 2x.
andf(x) = 2.
AR extreme point, f(x) = 0
2x = 0
x = 0.
When x = 0, f(0) = 2 > 0.
∴x = 0 is a point of local minima and value of local minimum is given by f(0) = 02 = 0.
(ii) g(x) = x3 3x
A(ii)
we have, g(x) = x3- 3x
g'(x) = 3x2- 3
g''(x) = 6x.
At extreme point,
g'(x) = 0
3x2- 3 = 0.
3(x2- 1) = 0 ⇒ 3(x - 1)(x + 1) = 0.
x = 1 or x = -1.
At x = 1, g"(1) = 6.1 = 6 > 0.
So, x = 1 is a point of local minima and value of local minimum is given by g(1) = 13- 3.1 = 1 - 3 = - 2.
And at x = -1, g"( -1) = 6 ( -1) = 6 < 0.
So, x = -1 is a point of local minima and value of local minimum is given by
g(- 1) = (- 1)3- 3(- 1) = 1
...more(i) we have, f(x) = x2.
f(x) = 2x.
andf(x) = 2.
AR extreme point, f(x) = 0
2x = 0
x = 0.
When x = 0, f(0) = 2 > 0.
∴x = 0 is a point of local minima and value of local minimum is given by f(0) = 02 = 0.
(ii) g(x) = x3 3x
A(ii)
we have, g(x) = x3- 3x
g'(x) = 3x2- 3
g''(x) = 6x.
At extreme point,
g'(x) = 0
3x2- 3 = 0.
3(x2- 1) = 0 ⇒ 3(x - 1)(x + 1) = 0.
x = 1 or x = -1.
At x = 1, g"(1) = 6.1 = 6 > 0.
So, x = 1 is a point of local minima and value of local minimum is given by g(1) = 13- 3.1 = 1 - 3 = - 2.
And at x = -1, g"( -1) = 6 ( -1) = 6 < 0.
So, x = -1 is a point of local minima and value of local minimum is given by
g(- 1) = (- 1)3- 3(- 1) = 1 + 3 = 2.
(iii)
A(iii)
we have, h(x) = sin x + cos x.
h'(x) = cos x - sin x
h'(x) = -sin x - cos x.
At extreme points,
h'(x) = 0
cosx - sin x = 0
cosx = sin x
1 = tan x
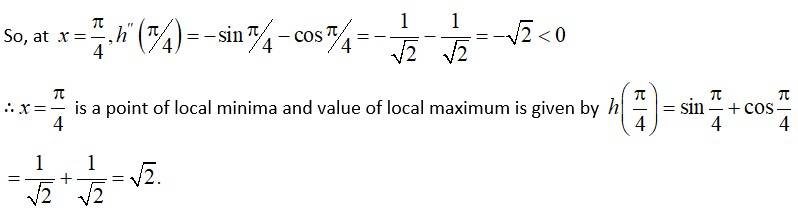
(iv)
A(iv)
we have, f(x) = sin x cos x.
f(x) = cos x + sin x
f(x) = sin x + cos x.
At extreme points,
f(x) = 0
cosx + sin x = 0.
IInd quadrate or IIIth quadrate
 (v) f(x) = x3- 6x2 + 9x + 15.
(v) f(x) = x3- 6x2 + 9x + 15.A(v)
we have, f(x) = x3- 6x2 + 9x + 15.
f(x) = 3x2- 12x + 9.
f'(x) = 6x - 12.
At extreme point, f'(x) = 0.
3x2- 12x + 9 = 0.
x2- 4x + 3 = 0
x2-x - 3x + 3 = 0
x(x - 1) -3(x - 1) = 0
(x - 1)(x - 3) = 0
x = 1 or x = 3.
At, x = 1,f"(1) = 6 × 1 - 12 = 6 - 12 = - 6 < 0
∴x = 1 is a point of local maxima and the value of local
Maximum is given by f(1) = 13- 6(1)2 + 9(1) + 15
= 1 - 6 + 9 + 15
= 19.
And at x = 3,f"(3) = 6 × 3 - 12 = 18 - 12 = 6 > 0
∴x = 3 is a point of local minima and the value of
local minimum is given by f (3) = 33- 6(3)2 + 9(3) + 15.
= 27 - 54 + 27 + 15.
= 15.
(vi)
A(vi)
We have,
At, extreme point, g'(x) = 0
x = -2 or x = 2
Given, that x > 0, hence we have x = 2.
At, x = 2,
∴x = 2 is a point of local minima and value of local
Minimum is given by g(2) =
(vii)
A(vii)
Given,
At extreme points, g'(x) = 0.
x = 0.
At, x = 0,
∴x = 0 is a point of local maxima and value of local maximum is given by
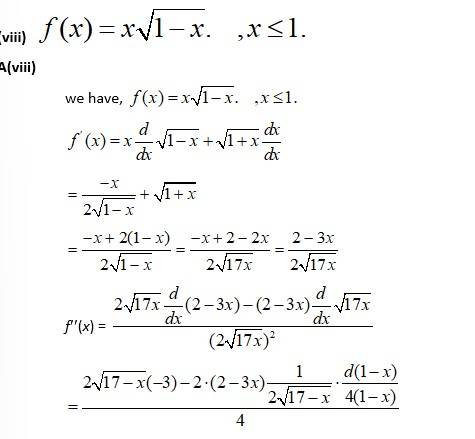
 less
less<p><strong>(i) </strong>we have, f(x) = <em>x</em><sup>2</sup>.</p><p>f(x) = 2x.</p><p>andf(x) = 2.</p><p>AR extreme point, f(x) = 0</p><p>2x = 0</p><p>x = 0.</p><p>When x = 0, f(0) = 2 > 0.</p><p>∴x = 0 is a point of local minima and value of local minimum is given by f(0) = 0<sup>2</sup> = 0.</p><p><strong>(ii)</strong> g(x) = <em>x</em><sup>3</sup> 3x</p><p>A(ii)</p><p>we have, g(x) = <em>x</em><sup>3</sup>- 3<em>x</em></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> g'(x) = 3<em>x</em><sup>2</sup>- 3</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> g''(x) = 6x.</p><p>At extreme point,</p><p>g'(x) = 0</p><p>3<em>x</em><sup>2</sup>- 3 = 0.</p><p>3(<em>x</em><sup>2</sup>- 1) = 0 ⇒ 3(x - 1)(x + 1) = 0.</p><p>x = 1 or x = -1.</p><p>At x = 1, g"(1) = 6.1 = 6 > 0.</p><p>So, x = 1 is a point of local minima and value of local minimum is given by g(1) = 1<sup>3</sup>- 3.1 = 1 - 3 = - 2.</p><p>And at x = -1, g"( -1) = 6 ( -1) = 6 < 0.</p><p>So, x = -1 is a point of local minima and value of local minimum is given by</p><p>g(- 1) = (- 1)<sup>3</sup>- 3(- 1) = 1 + 3 = 2.</p><p><strong>(iii)</strong> <span title="Click to copy mathml"><math><mrow><mi>h</mi><mrow><mo>(</mo><mrow><mi>x</mi></mrow><mo>)</mo></mrow><mo>=</mo><mi>s</mi><mi>i</mi><mi>n</mi><mi>x</mi><mo>+</mo><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi><mo>.</mo><mn>0</mn><mo><</mo><mi>x</mi><mo><</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math></span></p><p>A(iii)</p><p>we have, h(x) = sin x + cos x.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> h'(x) = cos x - sin x</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> h'(x) = -sin x - cos x.</p><p>At extreme points,</p><p>h'(x) = 0</p><p>cosx - sin x = 0</p><p>cosx = sin x</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mtext> </mtext><mfrac><mrow><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi></mrow><mrow><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi></mrow></mfrac><mo>=</mo><mfrac><mrow><mi>s</mi><mi>i</mi><mi>n</mi><mi>x</mi></mrow><mrow><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> 1 = tan x</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mi>t</mi><mi>a</mi><mi>n</mi><mi>x</mi><mo>=</mo><mi>t</mi><mi>a</mi><mi>n</mi><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mi>x</mi><mo>=</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mo>.</mo></mrow></math></span></p><div><div><picture><source srcset="https://images.shiksha.com/mediadata/images/articles/1734068563phpiAlP6W_480x360.jpeg" media="(max-width: 500px)"><img src="https://images.shiksha.com/mediadata/images/articles/1734068563phpiAlP6W.jpeg" alt="" width="502" height="132"></picture></div></div><p><strong>(iv) </strong><span title="Click to copy mathml"><math><mrow><mi>f</mi><mrow><mo>(</mo><mrow><mi>x</mi></mrow><mo>)</mo></mrow><mo>=</mo><mi>s</mi><mi>i</mi><mi>n</mi><mi>x</mi><mo>−</mo><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi><mo>,</mo><mn>0</mn><mo><</mo><mi>x</mi><mo><</mo><mn>2</mn><mi>π</mi></mrow></math></span></p><p>A(iv)</p><p>we have, f(x) = sin x cos x.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> f(x) = cos x + sin x</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> f(x) = sin x + cos x.</p><p>At extreme points,</p><p>f(x) = 0</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> cosx + sin x = 0.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mfrac><mrow><mi>s</mi><mi>i</mi><mi>n</mi><mi>x</mi></mrow><mrow><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi></mrow></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi></mrow><mrow><mi>c</mi><mi>o</mi><mi>s</mi><mi>x</mi></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mi>t</mi><mi>a</mi><mi>n</mi><mi>x</mi><mo>=</mo><mo>−</mo><mn>1</mn><mo>=</mo><mo>−</mo><mi>t</mi><mi>a</mi><mi>n</mi><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mo>=</mo><mi>t</mi><mi>a</mi><mi>n</mi><mrow><mo>(</mo><mrow><mi>π</mi><mo>−</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow><mo>=</mo><mi>t</mi><mi>a</mi><mi>n</mi><mrow><mo>(</mo><mrow><mn>2</mn><mi>π</mi><mo>−</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>∴</mo><mi>x</mi><mo>=</mo><mrow><mo>(</mo><mrow><mi>π</mi><mo>−</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow></mrow></math></span> IInd quadrate or <span title="Click to copy mathml"><math><mrow><mrow><mo>(</mo><mrow><mn>2</mn><mi>π</mi><mo>−</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow></mrow></math></span> IIIth quadrate</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mi>x</mi><mo>=</mo><mfrac><mrow><mn>4</mn><mi>π</mi><mo>−</mo><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mfrac><mrow><mn>8</mn><mi>x</mi><mo>−</mo><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mi>x</mi><mo>=</mo><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>o</mi><mi>r</mi><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>x</mi><mo>=</mo><mfrac><mrow><mi>f</mi><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mo>.</mo></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mi>A</mi><mi>t</mi><mtext> </mtext><mtext> </mtext><mi>x</mi><mo>=</mo><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mo>,</mo><msup><mrow><mi>f</mi></mrow><mrow><mo>′</mo><mo>′</mo></mrow></msup><mrow><mo>(</mo><mrow><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow><mo>=</mo><mo>−</mo><mi>s</mi><mi>i</mi><mi>n</mi><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mo>+</mo><mi>c</mi><mi>o</mi><mi>s</mi><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>=</mo><mo>−</mo><mi>s</mi><mi>i</mi><mi>n</mi><mrow><mo>(</mo><mrow><mi>π</mi><mo>−</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow><mo>+</mo><mi>c</mi><mi>o</mi><mi>s</mi><mrow><mo>(</mo><mrow><mi>π</mi><mo>−</mo><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mo>)</mo></mrow></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>=</mo><mo>−</mo><mi>s</mi><mi>i</mi><mi>n</mi><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac><mo>−</mo><mi>c</mi><mi>o</mi><mi>t</mi><mfrac><mrow><mi>π</mi></mrow><mrow><mn>4</mn></mrow></mfrac></mrow></math></span><span title="Click to copy mathml"><br></span></p><div><div><picture><source srcset="https://images.shiksha.com/mediadata/images/articles/1734068728phpwMIpcn_480x360.jpeg" media="(max-width: 500px)"><img src="https://images.shiksha.com/mediadata/images/articles/1734068728phpwMIpcn.jpeg" alt="" width="426" height="371"></picture></div><div><strong>(v)</strong> f(x) = <em>x</em><sup>3</sup>- 6<em>x</em><sup>2</sup> + 9<em>x</em> + 15.</div></div><p>A(v)</p><p>we have, f(x) = <em>x</em><sup>3</sup>- 6<em>x</em><sup>2</sup> + 9<em>x</em> + 15.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> f(x) = 3<em>x</em><sup>2</sup>- 12<em>x</em> + 9.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> f'(x) = 6x - 12.</p><p>At extreme point, f'(x) = 0.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> 3<em>x</em><sup>2</sup>- 12<em>x</em> + 9 = 0.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> <em>x</em><sup>2</sup>- 4<em>x</em> + 3 = 0</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> <em>x</em><sup>2</sup>-<em>x </em>- 3<em>x</em> + 3 = 0</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> x(x - 1) -3(x - 1) = 0</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> (x - 1)(x - 3) = 0</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> x = 1 or x = 3.</p><p>At, x = 1,f"(1) = 6 × 1 - 12 = 6 - 12 = - 6 < 0</p><p>∴x = 1 is a point of local maxima and the value of local</p><p>Maximum is given by f(1) = 1<sup>3</sup>- 6(1)<sup>2</sup> + 9(1) + 15</p><p>= 1 - 6 + 9 + 15</p><p>= 19.</p><p>And at x = 3,f"(3) = 6 × 3 - 12 = 18 - 12 = 6 > 0</p><p>∴x = 3 is a point of local minima and the value of</p><p>local minimum is given by f (3) = 3<sup>3</sup>- 6(3)<sup>2</sup> + 9(3) + 15.</p><p>= 27 - 54 + 27 + 15.</p><p>= 15.</p><p><strong>(vi)</strong> <span title="Click to copy mathml"><math><mrow><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>+</mo><mfrac><mrow><mn>2</mn></mrow><mrow><mi>x</mi></mrow></mfrac><mo>,</mo><mi>x</mi><mo>></mo><mn>0</mn></mrow></math></span></p><p>A(vi)</p><p>We have, <span title="Click to copy mathml"><math><mrow><mi>g</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>+</mo><mfrac><mrow><mn>2</mn></mrow><mrow><mi>x</mi></mrow></mfrac><mo>,</mo><mi>x</mi><mo>></mo><mn>0</mn></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mtext> </mtext><msup><mrow><mi>g</mi></mrow><mrow><mo>′</mo></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>−</mo><mfrac><mrow><mn>2</mn></mrow><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mi>g</mi><msup><mrow><mi>g</mi></mrow><mrow><mo>′</mo><mi>z</mi></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>−</mo><mn>4</mn></mrow><mrow><mn>2</mn><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac><mo>=</mo><mfrac><mrow><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mn>2</mn><mo stretchy="false">)</mo></mrow><mrow><mn>2</mn><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><msup><mrow><mi>g</mi></mrow><mrow><mo>′</mo><mo>′</mo></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>4</mn></mrow><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></mfrac><mo>.</mo></mrow></math></span></p><p>At, extreme point, g'(x) = 0</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mfrac><mrow><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mn>2</mn><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo stretchy="false">)</mo></mrow><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac><mo>=</mo><mn>0</mn></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> x = -2 or x = 2</p><p>Given, that x > 0, hence we have x = 2.</p><p>At, x = 2, <span title="Click to copy mathml"><math><mrow><msup><mrow><mover accent="true"><mi>g</mi><mo>?</mo></mover></mrow><mrow><mo>′</mo></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>4</mn></mrow><mrow><msup><mrow><mn>2</mn></mrow><mrow><mn>3</mn></mrow></msup></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>4</mn></mrow><mrow><mn>8</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>></mo><mn>0</mn></mrow></math></span></p><p>∴x = 2 is a point of local minima and value of local</p><p>Minimum is given by g(2) = <span title="Click to copy mathml"><math><mrow><mfrac><mrow><mn>2</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>+</mo><mfrac><mrow><mn>2</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>=</mo><mn>1</mn><mo>+</mo><mn>1</mn><mo>=</mo><mn>2</mn><mo>.</mo></mrow></math></span></p><p><strong>(vii)</strong> <span title="Click to copy mathml"><math><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow></mfrac></mrow></math></span></p><p>A(vii)</p><p>Given, <span title="Click to copy mathml"><math><mrow><mi>f</mi><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><msup><mrow><mi>g</mi></mrow><mrow><mo>′</mo></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mo>−</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mi>x</mi></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac><mo>.</mo></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><msup><mrow><mi>g</mi></mrow><mrow><mo>′</mo><mo>′</mo></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mo>−</mo><mrow><mo>[</mo><mrow><mfrac><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><mn>2</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi><mfrac><mrow><mi>d</mi></mrow><mrow><mi>d</mi><mi>x</mi></mrow></mfrac><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>4</mn></mrow></msup></mrow></mfrac></mrow><mo>]</mo></mrow></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>=</mo><mfrac><mrow><mo>−</mo><mrow><mo>[</mo><mrow><mn>2</mn><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mo>−</mo><mn>2</mn><mi>x</mi><mo>⋅</mo><mn>2</mn><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow><mo>⋅</mo><mn>2</mn><mi>x</mi></mrow><mo>]</mo></mrow></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>4</mn></mrow></msup></mrow></mfrac><mo>.</mo></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>=</mo><mfrac><mrow><mo>−</mo><mrow><mo>[</mo><mrow><mn>2</mn><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mrow><mo>[</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn><mo>−</mo><mn>4</mn><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo>]</mo></mrow></mrow><mo>]</mo></mrow></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>4</mn></mrow></msup></mrow></mfrac></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow><mrow><mo>(</mo><mrow><mn>2</mn><mo>−</mo><mn>3</mn><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo>)</mo></mrow></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>4</mn></mrow></msup></mrow></mfrac><mo>=</mo><mo>−</mo><mfrac><mrow><mn>2</mn><mrow><mo>(</mo><mrow><mn>2</mn><mo>−</mo><mn>3</mn><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo>)</mo></mrow></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>3</mn></mrow></msup></mrow></mfrac><mo>.</mo></mrow></math></span></p><p>At extreme points, g'(x) = 0.</p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mi>x</mi></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></mfrac><mo>=</mo><mn>0</mn><mo>.</mo></mrow></math></span></p><p><span title="Click to copy mathml"><math><mrow><mo>⇒</mo></mrow></math></span> x = 0.</p><p>At, x = 0, <span title="Click to copy mathml"><math><mrow><msup><mrow><mi>g</mi></mrow><mrow><mo>′</mo><mo>′</mo></mrow></msup><mo stretchy="false">(</mo><mi>x</mi><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mrow><mo>(</mo><mrow><mn>2</mn><mo>−</mo><mn>2</mn><mo>×</mo><msup><mrow><mn>0</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo>)</mo></mrow></mrow><mrow><msup><mrow><mrow><mo>(</mo><mrow><msup><mrow><mn>0</mn></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow><mo>)</mo></mrow></mrow><mrow><mn>3</mn></mrow></msup></mrow></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mo stretchy="false">(</mo><mn>2</mn><mo>−</mo><mn>0</mn><mo stretchy="false">)</mo></mrow><mrow><msup><mrow><mn>2</mn></mrow><mrow><mn>3</mn></mrow></msup></mrow></mfrac><mo>=</mo><mo>−</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo><</mo><mn>0</mn></mrow></math></span></p><p>∴x = 0 is a point of local maxima and value of local maximum is given by <span title="Click to copy mathml"><math><mrow><mi>g</mi><mo stretchy="false">(</mo><mn>0</mn><mo stretchy="false">)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><msup><mrow><mn>0</mn></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><mn>2</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>.</mo></mrow></math></span></p><div><div><picture><source srcset="https://images.shiksha.com/mediadata/images/articles/1734069203phpSS4at0_480x360.jpeg" media="(max-width: 500px)"><img src="https://images.shiksha.com/mediadata/images/articles/1734069203phpSS4at0.jpeg" alt="" width="319" height="295"></picture></div></div><div><div><picture><img src="https://images.shiksha.com/mediadata/images/articles/1734069223phptw07x9.jpeg" alt="" width="389" height="462"></picture></div></div>
Similar Questions for you
y (x) = ∫? (2t² - 15t + 10)dt
dy/dx = 2x² - 15x + 10.
For tangent at (a, b), slope is m = dx/dy = 1 / (dy/dx) = 1 / (2a² - 15a + 10).
Given slope is -1/3.
2a² - 15a + 10 = -3
2a² - 15a + 13 = 0 (The provided solution has 2a²-15a+7=0, suggesting a different problem or a typo)
Following the image: 2a² - 15a + 7 = 0
(2a - 1) (a - 7) = 0
a = 1/2 or a = 7.
a = 1/2 Rejected as a > 1. So a = 7.
b = ∫? (2t² - 15t + 10)dt = [2t³/3 - 15t²/2 + 10t] from 0 to 7.
6b = [4t³ - 45t² + 60t] from 0 to 7 = 4 (7)³ - 45 (7)² + 60 (7) = 1372 - 2205 + 420 = -413.
|a + 6b| = |7 - 413| = |-406| = 406.
f' (c) = 1 + lnc = e/ (e-1)
lnc = e/ (e-1) - 1 = (e - (e-1)/ (e-1) = 1/ (e-1)
c = e^ (1/ (e-1)
Area
3x2 = 10
x = k
3k2 = 10
By truth table
So F1 (A, B, C) is not a tautology
Now again by truth table
So F2 (A, B) be a tautology.
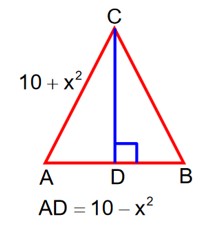
From option let it be isosceles where AB = AC then
=
Now ar
then
So .
Hence be equilateral having each side of length
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
Share Your College Life Experience
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Please select a topic from suggestions
or
Ask Current Students, Alumni & our Experts
