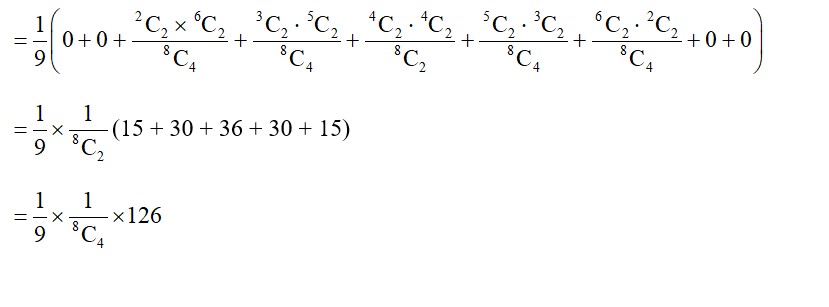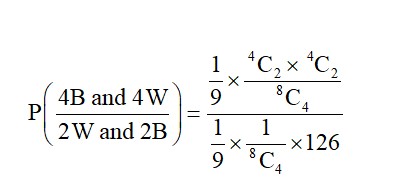Ask & Answer Question

Probability Ncert Solutions Maths class 12th Maths Class 12th Probability

88. Suppose we have four boxes A, B, C and D containing coloured marbles as given below:

Box

Marble colour

Red

White

Black

A

B

C

D

1

6

8

0

6

2

1

6

3

2

1

4

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A?, box B? box C?

3 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

4 months ago

88. Let R be the event of drawing the red marble.

Let EA, EB, and EC respectively denote the events of selecting the box A, B, and C.

Total number of marbles = 40

Number of red marbles = 15

P (R) = 15/40 = 3/8

Probability of drawing the red marble from box A is given by P (EA|R).

$? P (E_{A} | R) = \frac{P (E_{A} ? R)}{P (R)} = \frac{\frac{1}{40}}{\frac{3}{8}} = \frac{1}{15}$

Probability that the red marble is from box B is P (EB|R).

$? P (E_{B} | R) = \frac{P (E_{B} ? R)}{P (R)} = \frac{\frac{6}{40}}{\frac{3}{8}} = \frac{2}{5}$

Probability that the red marble is from box C is P (EC|R).

$? P (E_{C} | R) = \frac{P (E_{C} ? R)}{P (R)} = \frac{\frac{8}{40}}{\frac{3}{8}} = \frac{8}{15}$

0 Upvotes 0 Downvotes

Similar Questions for you

Let a die rolled till 2 is obtained. The probability that 2 obtained on even numbered toss is equal to

alok kumar singh

P (2 obtained on even numbered toss) = k (let)

P (2) = $\frac{1}{6}$

P ( $\bar{2}$ )= $\frac{5}{6}$

$k = \frac{5}{6} \times \frac{1}{6} + {(\frac{5}{6})}^{3} \times \frac{1}{6} + {(\frac{5}{6})}^{5} \times \frac{1}{6} + . . .$

$= \frac{\frac{5}{6} \times \frac{1}{6}}{1 - {(\frac{5}{6})}^{2}}$

$= \frac{5}{11}$

Given set S = {0, 1, 2, 3, ….., 10}. If a random ordered pair (x, y) of elements of S is chosen, then find probability that |x – y| > 5

alok kumar singh

If x = 0, y = 6, 7, 8, 9, 10

If x = 1, y = 7, 8, 9, 10

If x = 2, y = 8, 9, 10

If x = 3, y = 9, 10

If x = 4, y = 10

If x = 5, y = no possible value

Total possible ways = (5 + 4 + 3 + 2 + 1) * 2

= 30

Required probability $= \frac{30}{11 * 11} = \frac{30}{121}$

A bag contains 8 balls (black and white). If four balls are chosen without replacement then 2W and 2B are found then the probability that number of white and black balls are same in bag is equal to

alok kumar singh

P (2W and 2B) = P (2B, 6W) × P (2W and 2B)

+ P (3B, 5W) × P (2W and 2B)

+ P (4B, 4W) × P (2W and 2B)

+ P (5B, 3W) × P (2W and 2B)

+ P (6B, 2W) × P (2W and 2B)

(15 + 30 + 36 + 30 + 15)

$= \frac{36}{126}$

$= \frac{18}{63}$

$= \frac{6}{21}$

$= \frac{2}{7}$

A coin is biased such that head has two chances than tails, what is the probability of getting 2 heads and 1 tail?

alok kumar singh

Let probability of tail is $\frac{1}{3}$

⇒ Probability of getting head = $\frac{2}{3}$

∴ Probability of getting 2 heads and 1 tail

$= (\frac{2}{3} \times \frac{2}{3} \times \frac{1}{3}) \times 3$

$= \frac{4}{27} \times 3$

$= \frac{4}{9}$

The coefficients a, b and c of the quadratic equation, ax² + bx + c = 0 are obtained by throwing a dice three times. The probability that this equation has equal roots is:

Vishal Baghel

ax² + bx + c = 0

D = b² – 4ac

D = 0

b² – 4ac = 0

b² = 4ac

(i) AC = 1, b = 2 (1, 2, 1) is one way

(ii) AC = 4, b = 4

$\begin{array}{l} a = 4 c = 1 \\ a = 2 c = 2 \\ a = 1 c = 4 \end{array}} 3 w a y s$

(iii) AC = 9, b = 6, a = 3, c = 3 is one way

1 + 3 + 1 = 5 way

Required probability = $\frac{5}{216}$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question