Consider a hyperbola H: x² - 2y² = 4. Let the tangent at a point P(4, √6) meet the x-axis at Q and latus rectum at R(x₁, y₁), x₁ > 0. If F is a focus of H which is nearer to the point P, then the area of ∆QFR is equal to :

$?$ ae = 2b

$\frac{4b^2}{a^2}=e^2$  

Or 4 (1 – e²) = e²

4 = 5e² -> $e=\frac{2}{\sqrt[]{5}}$

If two circles intersect at two distinct points

->|r₁ – r₂| < C₁C₂ < r₁ + r₂

| r – 2| <  $\sqrt[]{9+16}$ < r + 2

|r – 2| < 5                     and r + 2 > 5

–5 < r – 2 < 5                    r > 3                      … (2)

–3 < r < 7                                                        … (1)

From (1) and (2)

3 < r < 7

x² – y² cosec²q = 5 $\frac{x^2}{1}-\frac{y^2}{si{n}^2\theta }=5$                        

x² cosec²q + y² = 5  $\frac{x^2}{si{n}^2\theta }+\frac{y^2}{1}=5$        

$e_H=\sqrt[]{7}{e}_e$                  

and $e_H=\sqrt[]{1+\frac{si{n}^2\theta }{1}}$ &n

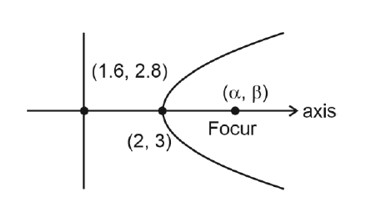
Slope of axis = $\frac{1}{2}$

$y-3=\frac{1}{2}\left(x-2\right)$              

⇒ 2y – 6 = x – 2

⇒ 2y – x – 4 = 0

2x + y – 6 = 0

4x + 2y – 12 = 0

            α + 1.6 = 4 ⇒ α = 2.4

            β + 2.8 = 6 ⇒

K $=\frac{4\sqrt[]{3}}{\sqrt[]{3}x+y}$ $\frac{\text{exception 25:}}{\text{exception 25:}}$

K = $\frac{\sqrt[]{3}x-y}{4\sqrt[]{3}}$ $\frac{\text{exception 25:}}{\text{exception 25:}}$

$\therefore \frac{4\sqrt[]{3}}{\sqrt[]{3}x+y}=\frac{\sqrt[]{3}x-y}{4\sqrt[]{3}}$

$\frac{x^2}{16}-\frac{y^2}{48}=1$

48 = 16 (e2 – 1)

$e=\sqrt[]{4}=2$