If the minimum and the maximum values of the function f: [-π/2, π/2] → R, defined by f(θ) = |-sin²θ -1 -sin²θ; -cos²θ -1 -cos²θ; 12 10 -2| are m and M respectively, then the ordered pair (m, M) is equal to:

$f\text{'}\left(x\right)=\frac{n_1\cdot f\left(x\right)}{x-3}+n_2\cdot \frac{f\left(x\right)}{x-5}$

$=\frac{f\left(x\right)\cdot \left(n_1+n_2\right)}{\left(x-3\right)\left(x-5\right)}\left(x-\frac{\left(5n_1+3n_2\right)}{n_1+n_2}\right)$

$f\text{'}\left(x\right)={\left(x-3\right)}^{n_1-1}\cdot {\left(x-5\right)}^{n_2-1}\cdot \left(n_1+n_2\right)\left(x-\frac{\left(5n_1+3n_2\right)}{n_1+n_{2l}}\right)$

option (C) is incorrect, there will be minima.

$f\left(x\right)=\left|x^2-3x-2\right|-x$

$=\left|\left(x-\frac{3-\sqrt[]{17}}{2}\right)\left(x-\frac{3+\sqrt[]{17}}{2}\right)\right|-x$

$\Rightarrow f\left(x\right)=\left[\begin{array}{cc}\hfill x^2-4x-2;-1\le x\le \frac{3-\sqrt[]{17}}{2}\hfill & \hfill -x^2+2x+2;\frac{3-\sqrt[]{17}}{2}<x\le 2\hfill \end{array}\right]$

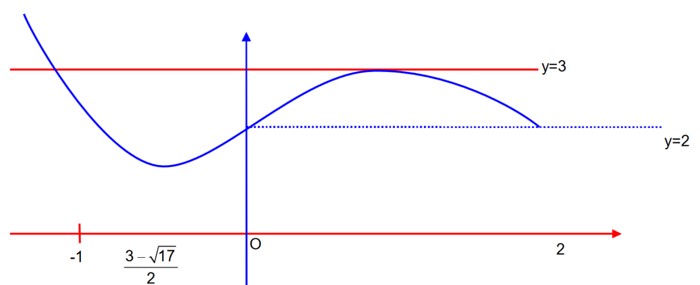
absolute minimum $f\left(\frac{3-\sqrt[]{17}}{2}\right)=\frac{-3+\sqrt[]{17}}{2}$  

 absolute maximum = 3

$\therefore sum3+\frac{-3+\sqrt[]{17}}{2}=\frac{3+\sqrt[]{17}}{2}$  

$f\left(x\right)=\{\begin{array}{cc}\hfill x^3-x^2+10x-7,\hfill & \hfill x\le 1\hfill \\ \hfill -2x+lo{g}_2\left(b^2-4\right),\hfill & \hfill x>1\hfill \end{array}$  

If f(x) has maximum value at x = 1 then

$f\left(1\right)\le f\left(1\right)\Rightarrow -2+lo{g}_2\left(b^2-4\right)\le 1-1+10-7$

$\Rightarrow lo{g}_2\left(b^2-4\right)\le 5\Rightarrow 0<b^2-4\le 32$

$\Rightarrow b^2-4>0\Rightarrow b\in \left(-\infty ,-2\right)\cup \left(2,\infty \right)$         ……..(i)

$And{b}^2-4\le 32\Rightarrow b\in \left[-6,6\right]$                      ……..(ii)

From (i) and (ii) we get  $b\in [-6,-2)\cup (2,6]$  

OP² = x² = y²

y = e^x, y’ = e^x,

slope of normal =  $-\frac{1}{e^x}$

$\frac{y}{x}=-\frac{1}{e^x}$    

$-\frac{1}{e^x}=\frac{e^x}{x}\Rightarrow -x=e^{2x}$      

By hit and trial we get  $x=-\frac{2}{5}$

$P\equiv \left(-\frac{2}{5},e^{-2/5}\right)$

$OP=\sqrt[]{\frac{4}{25}+e^{-4/5}}\Rightarrow O{P}^2=\frac{14}{25}=\frac{m}{n}$

c = -5, a = 2, b = 1