Search Colleges, Courses, Exams, Questions and Articles

Ask a query on 8879100846 Ask Login | Sign Up

 

 

› Ask & Answer › Question

Let a circle C of radius 5 lie below the x-axis. The line L1 : 4x + 3y + 2 = 0 passes through the centre P of the circle C and intersects the line L2 : 3x – 4y – 11 = 0 at Q. The line L2 touches C at the point Q. Then the distance of P from the line 5x – 12y + 51 = 0 is……….

0 3 Views | Posted 2 months ago
Asked by Shiksha User

  • 1 Answer

  • P

    Answered by

    Payal Gupta | Contributor-Level 10

    2 months ago

    L 1 : 4 x + 3 y + 2 = 0  

    L 2 : 3 x − 4 y − 1 1 = 0               

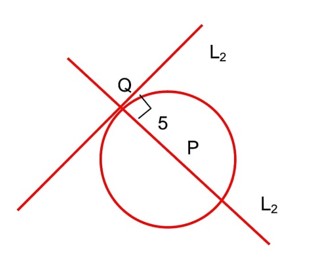
    Since circle C touches the line L2 at Q intersection point L1 and L2 is (1, -2)

    P lies of L1

    ∴ P ( x , − 1 3 ( 2 + 4 x ) )               

    Now,

    PQ = 5 ? (x – 1)2 + ( 4 x + 2 3 − 2 ) 2 = 2 5  

    ⇒ x = 4 , − 2                     

    ? The circle lies below the axis

    y = -6

    p (4, -6)

    Now distance of P from 5x – 12 y + 51 = 0

    = | 2 0 + 7 2 + 5 1 1 3 | = 1 4 3 1 3 = 1 1                

Similar Questions for you

The distance between the two points A and A’ which lie on y = 2 such that both the line segments AB and A’B (where B is the point (2, 3)) subtend angle π4 at the origin, is equal to:
A
alok kumar singh

Let A, A’ be (, 2) AB and A’B subtends π4 angle at (0, 0) slope of OA = 2α

 

slope of OB = 32

tanπ4=|2α−321+2α⋅32|

⇒1+3α=± (4−3α2α)

⇒α+3α=± (4−3α2α)⇒α=10,  −25

now distance between A’A, (10, 2) &  (−25, 2)is  525

The equations of the sides AB, BC and CA of a triangle ABC are 2x + y = 0, x + py = 15a and x – y = 3 respectively. If its orthocenter is (2, a), −12<a<2, then p is equal to…………
V
Vishal Baghel

Slope of AH = a+21 slope of BC = −1p∴p=a+2 ∴C (18p−30p+1, 15p−33p+1)

slope of HC = 16p−p2−3116p−32

slope of BC × slope of HC = -1 p = 3 or 5

hence p = 3 is only possible value.

A point P moves so that the sum of squares of its distances from the points (1, 2) and (2, 1) is 14. Let f(x, y) = 0 be the locus of P, which intersects the x-axis at the points A , B and the y-axis at the points C, D. Then the area of the quadrilateral ACBD is equal to:
V
Vishal Baghel

Let point P : (h, k)

Therefore according to question,   (h−1)2+ (k−2)2+ (h+2)2+ (k−1)2=14

∴ locus of P (h, k) is x2+y2+x−3y−2=0

Now intersection with x – axis are x2+x−2=0⇒x=−2, 1

Now intersection with y – axis are y2−3y−2=0⇒y=3±172

Therefore are of the quadrilateral ABCD is = 12 (|x1|+|x2|) (|y1|+|y2|)=12×3×17=3172

Let P and Q be any points on the curves (x – 1)2 + (y + 1)2 = 1 and y = x2, respectively. The distance between P and Q is minimum for some vale of the abscissa of P in the interval
A
alok kumar singh

Let equation of normal to x2 = y at Q (t, t2) is x + 2ty = t + 2t3

It passes through the point (1, -1) so, 2t3 + 3t – 1 = 0

Let f(t) = 2t3 + 3t – 1 f   ( 1 4 ) f ( 1 3 ) < 0 ⇒ t ∈ ( 1 4 , 1 3 )

Let P(1 – sin q, -1 + cos q) ∴  slope of normal = slope of CP − 1 2 t = c o s θ − s i n θ ⇒ 2 t Þ = tan q according to question x = 1 − s i n θ = 1 − 2 t 1 + 4 t 2 = g ( t ) ∴ g ( t ) = 1 − 2 t 1 + 4 t 2 ,  

Þ g’(t) < 0 Þ g(t) is decreasing function in  t ∈ ( 1 4 , 1 3 ) ⇒ g ( t ) ∈ ( 0 . 4 4 0 , 0 . 4 8 5 ) ∈ ( 1 4 , 1 2 )

A triangle ABC lying in the first quadrant has two vertices as A(1,2) and B(3,1) . If ∠BAC=90∘ , and ar⁡(△ABC)=55 sq. units, then the abscissa of the vertex C is:
A
alok kumar singh

K-2h-11-23-1=-1⇒K=2h

? [? ABC]=55

⇒12 (5) (h-1)2+ (K-2)2=55

Get authentic answers from experts, students and alumni that you won't find anywhere else

Sign Up on Shiksha

On Shiksha, get access to

  • 65k Colleges
  • 1.2k Exams
  • 688k Reviews
  • 1800k Answers

Learn more about...

Share Your College Life Experience

Write a Review

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Ask Now
Community GuidelinesUser Points System
QuestionsDiscussionsTags
×
×

This website uses Cookies and related technologies for the site to function correctly and securely, improve & personalise your browsing experience, analyse traffic, and support our marketing efforts and serve the Core Purpose. By continuing to browse the site, you agree to Privacy Policy and Cookie Policy.

Need guidance on career and education? Ask our experts

Characters 0/140

The Answer must contain atleast 20 characters.

Add more details

Characters 0/300

The Answer must contain atleast 20 characters.

Keep it short & simple. Type complete word. Avoid abusive language. Next

Your Question

Edit

Add relevant tags to get quick responses. Cancel Post