Let the maximum area of the triangle that can be inscribed in the ellipse having one of its vertices at one end of the major axis of the ellipse and one of its sides parallel to the y-axis, be . Then the eccentricity of the ellipse is
Let the maximum area of the triangle that can be inscribed in the ellipse having one of its vertices at one end of the major axis of the ellipse and one of its sides parallel to the y-axis, be . Then the eccentricity of the ellipse is
Option 1 -
Option 2 -
Option 3 -
Option 4 -
-
1 Answer
-
Correct Option - 1
Detailed Solution: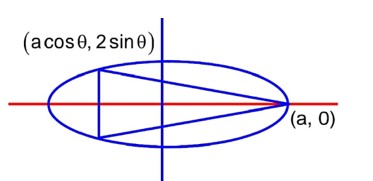
Similar Questions for you
ae = 2b
Or 4 (1 – e2) = e2
4 = 5e2 ->
If two circles intersect at two distinct points
->|r1 – r2| < C1C2 < r1 + r2
| r – 2| < < r + 2
|r – 2| < 5 and r + 2 > 5
–5 < r 2 < 5 r > 3 … (2)
–3 < r < 7 (1)
From (1) and (2)
3 < r < 7
x2 – y2 cosec2q = 5
x2 cosec2q + y2 = 5
and
->
1 + sin2q = 7 – 7 sin2q
->8sin2q = 6
->
->
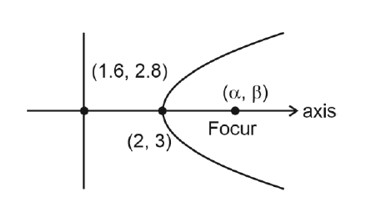
Slope of axis =
⇒ 2y – 6 = x – 2
⇒ 2y – x – 4 = 0
2x + y – 6 = 0
4x + 2y – 12 = 0
α + 1.6 = 4 ⇒ α = 2.4
β + 2.8 = 6 ⇒ β = 3.2
Ellipse passes through (2.4, 3.2)
⇒
Also
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
