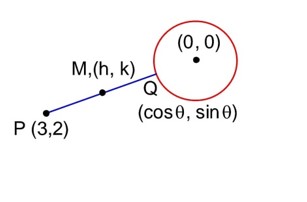
The line passes through the centre of circle x2 + y2 – 16x – 4y = 0, it interacts with the positive coordinate axis at A & B. Then find the minimum value of OA + OB, where O is origin.

(y – 2) = m (x – 8)⇒ x-intercept⇒ <!- [if gte mso 9]><xml> </xml><! [endif]-> ( − 2 m + 8 ) ⇒ y-intercept⇒ (–8m + 2)⇒ OA + OB = − 2 m 2 <!- [if gte mso 9]><xml> </xml><! [endif]-> + 8 – 8m + 2 f ' ( m ) = 2 m 2 − 8 = 0 <!- [if gte mso 9]><xml> </xml><! [endif]->-> m 2 = 1 4 -> m = − 1 2 -> f ( − 1 2 ) = 1 8 ->Minimum = 18

The line passes through the centre of circle x2 + y2 – 16x – 4y = 0, it interacts with the positive coordinate axis at A &amp; B. Then find the minimum value of OA + OB, where O is origin.

20

18

12

24

Ask & Answer Question

Maths NCERT Exemplar Solutions Class 11th Chapter Eight Straight Lines Ncert Solutions Maths class 11th Maths Class 11th

The line passes through the centre of circle x² + y² – 16x – 4y = 0, it interacts with the positive coordinate axis at A & B. Then find the minimum value of OA + OB, where O is origin.

Option 1 -

Option 2 -

Option 3 -

Option 4 -

2 Views | Posted a week ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

a week ago

Correct Option - 1

Detailed Solution:

(y – 2) = m (x – 8)

⇒ x-intercept

⇒ $(\frac{- 2}{m} + 8)$

⇒ y-intercept

⇒ (–8m + 2)

⇒ OA + OB = $\frac{- 2}{m^{2}}$ + 8 – 8m + 2

$f' (m) = \frac{2}{m^{2}} - 8 = 0$

-> $m^{2} = \frac{1}{4}$

-> $m = \frac{- 1}{2}$

-> $f (\frac{- 1}{2}) = 18$

->Minimum = 18

(y – 2) = m (x – 8)⇒   x-intercept⇒   <!- [if gte mso 9]><xml> <o:OLEObject Type="Embed" ProgID="Equation.DSMT4" ShapeID="_x0000_i1025" DrawAspect="Content" ObjectID="_1820304504"> </o:OLEObject></xml><! [endif]->  <math> <mrow> <mrow> <mo> (</mo> <mrow> <mfrac> <mrow> <mo>−</mo> <mn>2</mn> </mrow> <mrow> <mi>m</mi> </mrow> </mfrac> <mo>+</mo> <mn>8</mn> </mrow> <mo>)</mo> </mrow> </mrow> </math> ⇒   y-intercept⇒   (–8m + 2)⇒   OA + OB = <math> <mrow> <mfrac> <mrow> <mo>−</mo> <mn>2</mn> </mrow> <mrow> <msup> <mrow> <mi>m</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msup> </mrow> </mfrac> </mrow> </math> <!- [if gte mso 9]><xml> <o:OLEObject Type="Embed" ProgID="Equation.DSMT4" ShapeID="_x0000_i1026" DrawAspect="Content" ObjectID="_1820304505"> </o:OLEObject></xml><! [endif]-> + 8 – 8m + 2 <math> <mrow> <mi>f</mi> <mo>'</mo> <mrow> <mo> (</mo> <mrow> <mi>m</mi> </mrow> <mo>)</mo> </mrow> <mo>=</mo> <mfrac> <mrow> <mn>2</mn> </mrow> <mrow> <msup> <mrow> <mi>m</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msup> </mrow> </mfrac> <mo>−</mo> <mn>8</mn> <mo>=</mo> <mn>0</mn> </mrow> </math>  <!- [if gte mso 9]><xml> <o:OLEObject Type="Embed" ProgID="Equation.DSMT4" ShapeID="_x0000_i1027" DrawAspect="Content" ObjectID="_1820304506"> </o:OLEObject></xml><! [endif]->-> <math> <mrow> <msup> <mrow> <mi>m</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msup> <mo>=</mo> <mfrac> <mrow> <mn>1</mn> </mrow> <mrow> <mn>4</mn> </mrow> </mfrac> </mrow> </math> -> <math> <mrow> <mi>m</mi> <mo>=</mo> <mfrac> <mrow> <mo>−</mo> <mn>1</mn> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mrow> </math> -> <math> <mrow> <mi>f</mi> <mrow> <mo> (</mo> <mrow> <mfrac> <mrow> <mo>−</mo> <mn>1</mn> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mrow> <mo>)</mo> </mrow> <mo>=</mo> <mn>1</mn> <mn>8</mn> </mrow> </math> ->Minimum = 18

0 Upvotes 0 Downvotes

Similar Questions for you

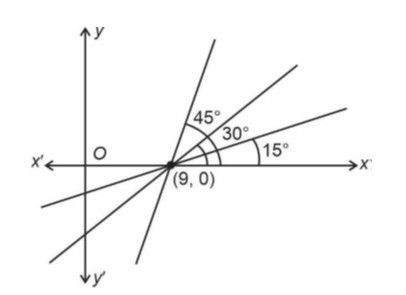
A line passes through (9, 0), making angle 30° with positive direction of x-axis. It is rotated by angle of 15° with respect to (9, 0). Then one of the equation of new line is

alok kumar singh

Eqⁿ : y – 0 = tan45° (x – 9) Þ y = (x – 9)

Option (B) is correct

If two circle x² + y² = 4 and x² + y² – 4lx + 9 = 0 intersect at two distinct points, then find the range of l.

alok kumar singh

|r₁ – r₂| < c₁c₂ < r₁ + r₂

-> $| 2 - \sqrt[]{4 λ^{2} - 9} | < | 2 λ | < 2 + \sqrt[]{4 λ^{2} - 9}$

$| 2 λ | - 2 < \sqrt[]{4 λ^{2} - 9}$

$4 λ^{2} + 4 - 8 | λ | < 4 λ^{2} - 9$

$λ > \frac{13}{8}, λ < - \frac{13}{8}$

$\sqrt[]{4 λ^{2} - 9} > 0$

$λ > \frac{3}{2}, λ < - \frac{3}{2}$

$λ \in (- \infty, - \frac{13}{8}) \cup (\frac{13}{8}, \infty)$

Now,

$| 2 - \sqrt[]{4 λ^{2} - 9} | < | 2 λ |$

$4 + 4 λ^{2} - 9 - 4 \sqrt[]{4 λ^{2} - 9} < 4 λ^{2}$

$4 \sqrt[]{4 λ^{2} - 9} > - 5 \Rightarrow λ \in R$

$λ \in (- \infty, - \frac{13}{8}) \cup (\frac{13}{8}, \infty)$

The image of the point (3, 5) in the line x – y + 1 = 0, lies on:

Vishal Baghel

Kindly consider the following figure

A man is walking on a straight line. The arithmetic mean of the reciprocals of the intercepts of the line on the coordinate axes is $\frac{1}{4} .$ Three stones A, B and C are placed at the point (1, 1), (2, 2) and (4, 4) respectively. Then which of these stones is / are on the path of the man?

Vishal Baghel

According to question,

$\frac{1}{2} (\frac{1}{a} + \frac{1}{b}) = \frac{1}{4}$

$\frac{1}{a} + \frac{1}{b} = \frac{1}{2} . . . . . . . . (i)$

Equation of required line is $\frac{x}{a} + \frac{y}{b} = 1$ $\frac{}{} \frac{}{}$

Obviously B (2, 2) satisfying condition (i)

If the locus of the mid-point of the line segment from the point (3, 2) to a point on the circle, x² + y² = 1 is a circle of radius r, then r is equal to:

alok kumar singh

$h = \frac{c o s θ + 3}{2}$

$k = \frac{s i n θ + 2}{2}$

-> $c o s θ = 2 h - 3 & s i n θ = 2 k - 2$

-> ${(h - 3 / 2)}^{2} + {(k - 1)}^{2} = \frac{1}{4}$

$∴$ circle of radius r = $\frac{1}{2}$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

The line passes through the centre of circle x² + y² – 16x – 4y = 0, it interacts with the positive coordinate axis at A & B. Then find the minimum value of OA + OB, where O is origin.

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question