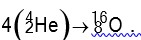13.1 (a) Two stable isotopes of lithium and have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes, and . Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of and 10.
13.1 (a) Two stable isotopes of lithium and have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes, and . Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of and 10.
-
1 Answer
-
13.1 Mass of lithium isotope, = 6.01512 u
Mass of lithium isotope, = 7.01600 u
Abundance of , = 7.5%
Abundance of , = 92.5%
The atomic mass of lithium atom is given as:
m = = = 6.940934 u
Mass of Boron isotope, = 10.01294 u
Mass of Boron isotope, = 11.00931 u
Let the abundance of be x % and that of be (100-x) %
The atomic mass of Boron atom is given as :
10.8111 =
1081.11 = 1100.931 - 0.99637x
x = 19.89 %
Hence the abundance of is 19.89 % and that of &nb
...more
Similar Questions for you
Q = [4 *4.0026 – 15.9994] *931.5 MeV
Q = 10.2 MeV
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers