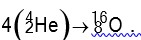13.12 Find the Q-value and the kinetic energy of the emitted -particle in the -decay of (a) and (b) . Given m ( = 226.02540 u, m ( = 222.01750 u, m ( = 220.01137 u, m ( = 216.00189 u.
13.12 Find the Q-value and the kinetic energy of the emitted -particle in the -decay of (a) and (b) . Given m ( = 226.02540 u, m ( = 222.01750 u, m ( = 220.01137 u, m ( = 216.00189 u.
-
1 Answer
-
13.12 particle decay of emits a helium nucleus. As a result, its mass number reduces to (226-4) 222 and its atomic number reduces to (88-2) 86.
+
Q value of emitted particle = (Sum of initial mass – Sum of final mass) , where
c = Speed of light.
It is given that
m ( = 226.02540 u
m ( = 222.01750 u
m ( = 4.002603 u
Q value = [(226.02540) – (222.01750 + 4.002603)]
= 5.297
But 1 u = 931.5 MeV/
Hence Q = 4.934 MeV
Kinetic energy of the particle = = 4.934= 4.85 MeV
particle decay
...more
Similar Questions for you
Q = [4 *4.0026 – 15.9994] *931.5 MeV
Q = 10.2 MeV
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers