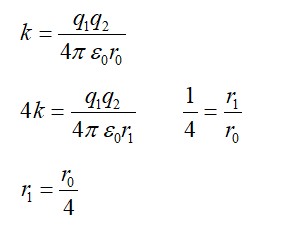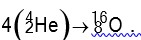13.13 The radionuclide decays according to =20.3 min. The maximum energy of the emitted positron is 0.960 MeV. Given the mass values: m ( = 11.011434 u and m ( ) = 11.009305 u, calculate Q and compare it with the maximum energy of the positron emitted.
13.13 The radionuclide decays according to =20.3 min. The maximum energy of the emitted positron is 0.960 MeV. Given the mass values: m ( = 11.011434 u and m ( ) = 11.009305 u, calculate Q and compare it with the maximum energy of the positron emitted.
-
1 Answer
-
13.13 The given values are
m ( = 11.011434 u and m ( ) = 11.009305 u
The given nuclear reaction:
Half life of nuclei, =20.3 min
The maximum energy possessed by the emitted positron = 0.960 MeV
The change in the Q-value (ΔQ) of the nuclear masses of the
ΔQ =
where
= Mass of an electron or positron = 0.000548 u
c = speed of the light
m’ = Respective nuclear masses
If atomic masses are used instead of nuclear masses, then we have to add 6 in the case of and 5 in the case of .
Hence the equation (1) reduces to
ΔQ =
=&nb
...more
Similar Questions for you
Q = [4 *4.0026 – 15.9994] *931.5 MeV
Q = 10.2 MeV
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers