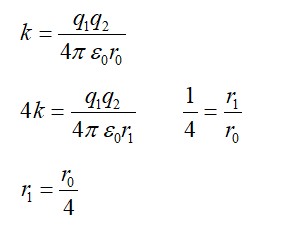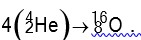13.28 Consider the D–T reaction (deuterium–tritium fusion)
(a) Calculate the energy released in MeV in this reaction from the data:
m(
=2.014102 u
m(
=3.016049 u
(b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction?
(Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzmann’s constant, T = absolute temperature.)
13.28 Consider the D–T reaction (deuterium–tritium fusion)
(a) Calculate the energy released in MeV in this reaction from the data:
m( =2.014102 u
m( =3.016049 u
(b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction?
(Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzmann’s constant, T = absolute temperature.)
-
1 Answer
-
13.28 The equation for deuterium-tritium fusion is given as:
It is given that
Mass of ( = 2.014102 u
Mass of ( , 3.016049 u
Mass of ( = 4.002603 u
Mass of ( = 1.008665 u
Q-value of the given D-T reaction is:
Q =
=
= 0.018883
= 17.59 MeV
Radius of the deuterium and tritium, r = 2 m
Distance between the centers of the nucleus when they touch each other,
d = r +r = 4 m
Charge on the deuterium and tritium nucleus = e
Hence the repulsive potential energy between the two nuclei is given as:
V =
Where,
= permittivity of free space
It is given that = 9 N
Hence, V = 9 = 5.76 J =
...more
Similar Questions for you
Q = [4 *4.0026 – 15.9994] *931.5 MeV
Q = 10.2 MeV
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers