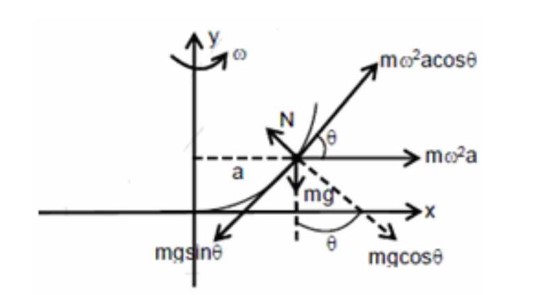
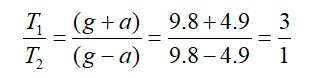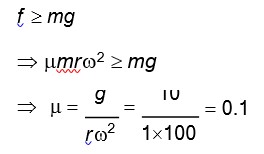A bead of mass m stays at point P(a,b) on a wire bent in the shape of a parabola y = Cx² and rotating with angular speed ω (see figure). The value of ω is (neglect friction) &lt;!-- [if !supportLineBreakNewLine]--&gt; &lt;!--[endif]--&gt;

2√(2gC)

√(2gC/ab)

Ask & Answer Question

Overview Physics Laws of Motion Physics Class 11th

A bead of mass m stays at point P(a,b) on a wire bent in the shape of a parabola y = Cx² and rotating with angular speed ω (see figure). The value of ω is (neglect friction)

Option 1 -

√(2gC/ab)

Option 2 -

√(2g/C)

Option 3 -

2√(2gC)

Option 4 -

2√(gC)

4 Views | Posted a month ago

Asked by Shiksha User

1 Answer

Answered by

alok kumar singh | Contributor-Level 10

a month ago

Correct Option - 3

Detailed Solution:

mω²acosθ = mgsinθ
ω = √ (gtanθ/a)
y = 4cx²

tanθ = dy/dx = 8xC
(tanθ)? , b = 8aC
ω = √ (g×8aC/a) = 2√ (2gC)

0 Upvotes 0 Downvotes

Similar Questions for you

A mass of 1 kg is suspended by a thread. It is lifted up with an acceleration of 4.9 ms^–2, and then lowered with an acceleration of 4.9 ms^–2 . The ratio of tensions in first case to second cases is (g = 9.8 ms^–2 )

alok kumar singh

T₁ = m (g + a)

T₂ = m (g - a)

Ball released from height 10 m strikes ground and rebounds height 5 m. Find impulse imparted by ground while collision, given mass of ball is 100 g. (Take g = 10 m/s²)

alok kumar singh

$v_{1} = \sqrt[]{2 g 10}$

$v_{2} = \sqrt[]{2 g 5}$

$\vec{l} = Δ \vec{p}$

$l = 0.1 {\sqrt[]{2 g 10} + \sqrt[]{2 g 5}}$

$= 0.1 {10 \sqrt[]{2} + 10}$

$= (\sqrt[]{2} + 1) N s$

A ball is projected from ground with initial momentum p at an angle q. What is the magnitude of net change in linear momentum when it reaches at maximum height of journey?

alok kumar singh

When an elevator is moving downward with a increasing speed, the apparent weight of a body inside elevator

alok kumar singh

Apparent weight = mg – ma

An insect of mass m = 2 g is inside a vertical drum of radius 1 m that is rotating with an angular velocity of 10 rad/s. If the insect does not fall off then the minimum coefficient of friction is