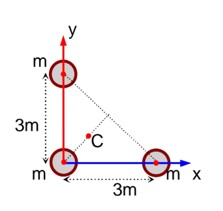
A body of mass 2 kg moving with a speed of 4 m/s, makes an elastic collision with another body at rest and continues to move in the original direction but with one fourth of its initial speed. The speed of the two body centre of mass is x/10 m/s. Then the value of x is _______ .

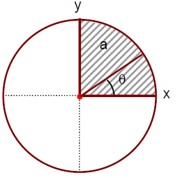
The x and y coordinates of the center of mass are given by:
x? = y? = 4a / 3π

$\left(\mathrm{0,3}\right)$

$\begin{array}{rr}& {\stackrel{?}{r}}_{\mathrm{c}\mathrm{m}}=\frac{1\times \left(\frac{\hat{i}}{2}+\hat{j}\right)+1\times \left(\hat{i}+\frac{5\hat{j}}{2}\right)}{2}\\ & {\stackrel{?}{r}}_{\mathrm{c}\mathrm{m}}=\frac{3}{4}\hat{i}+\frac{7}{4}\hat{j}\end{array}$

$\left(\mathrm{0,0}\right)$

$X_c=Y_c=\frac{m_1{x}_1+m_2{x}_2+m_3{x}_3}{m_1+m_2+m_3}=\frac{m\times 0+m\times 0+m\times 3}{3m}=1m$

$OC=X\sqrt[]{x_0^2+Y_c^2}=\sqrt[]{{\left(1\right)}^2+{\left(1\right)}^2}=\sqrt[]{2}m$

You should know that when the shift in the centre of mass occurs, you can use the principle of moments. With this logic, we can see the shift from the original body as the combination of two parts. The one that remains part and the other that is removed. The formula for the shift is the product of the mass removed and its distance of its centre of mass from the original centre of mass, which is divided by the mass of the remaining part.  

To study centre of mass, you need to follow these steps. 

• Learn the definition with examples. Most importantly, focus on visualising it. 
• Then approach the centre of mass formulas for discrete particles and continuous bodies.
• Practice finding the centre of mass for symmetrical and asymmetrical bodies. 
• Solve problems on the motion of centre of mass and its applications in collisions of particles.