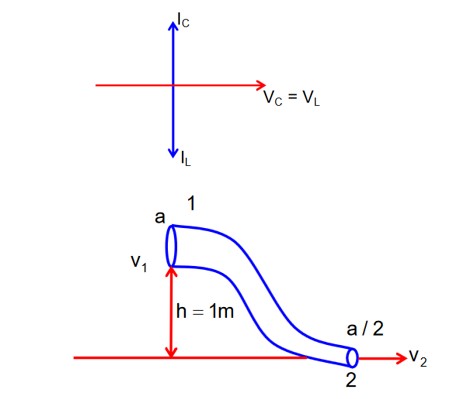
A fluid is flowing through a horizontal pipe of varying cross-section, with speed v ms⁻¹ at a point where the pressure is P Pascal. At another point where pressure is P/2 Pascal its speed is V ms⁻¹. If the density of the fluid is ρ kgm⁻³ and the flow is streamline, then V is equal to:

$\rho =800kg/m^3$

P₁ – P₂ = 4100 Pa

 Bernoulli’s question b/w (1) & (2)

$\frac{P_1}{\rho g}+\frac{v_1^2}{2g}+z_1=\frac{P_2}{\rho g}+\frac{v_2^2}{2g}+z_2$  

⇒  $\frac{P_1-P_2}{\rho g}+\frac{v_1^2}{2g}+1=\frac{v_2^2}{2g}+0$            -(1)

Equation of continuity

A₁v₁ = A₂v₂

v₂ = 2v₁                -(2)

from (1) & (2)

$\Rightarrow \frac{P_1-P_2}{\rho g}+\frac{v_1^2}{2g}+1=\frac{{\left(2v_1\right)}^2}{2g}$  

$\frac{4100}{800\times 10}+\frac{v_1^2}{2g}+1=\frac{4v_1^2}{2g}$  

$\frac{12100}{8000}=\frac{3v_1^2}{2g}$

$\Rightarrow v_1^2=\frac{2\times 10}{3}\times \frac{12100}{8000}$  

&nb