A particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration (a) is varying with time t as a = k2 rt2, where k is a constant. The power delivered to the particle by the force acting on it is given as
A particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration (a) is varying with time t as a = k2 rt2, where k is a constant. The power delivered to the particle by the force acting on it is given as
Option 1 -
zero
Option 2 -
mk2 r2 t2
Option 3 -
mk2 r2 t2
Option 4 -
mk2 rt
-
1 Answer
-
Correct Option - 3
Detailed Solution:a = k2rt2
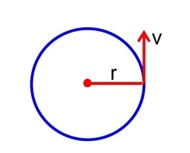
⇒ tangential force, Ft = mat = mkr
Note → Power delivered by centripetal force will be zero.
Similar Questions for you
Let 'x' be the value of one division on main scale
Let 'y' be the value of one division on vernier
Now given
50y = 49 x
Let 'h' be the height at which velocity becomes equal to magnitude of Acceleration
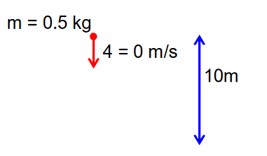
v = g = 10
v = u + at
10 = 0 + 10t
t = 1 sec
= 5m
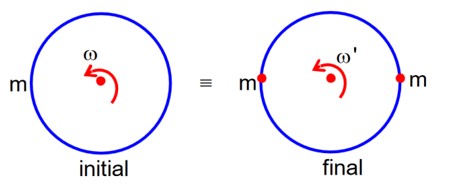
By conservation of Angular momentum
Li = Lf
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers